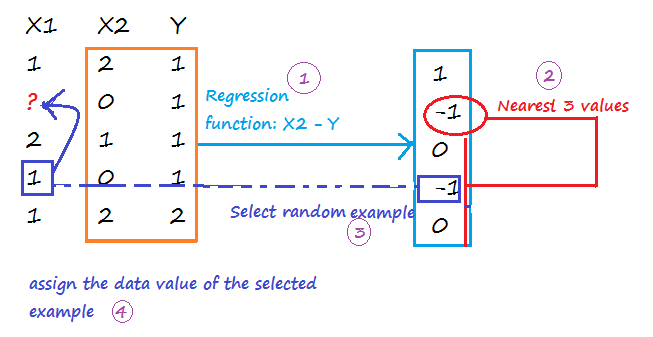
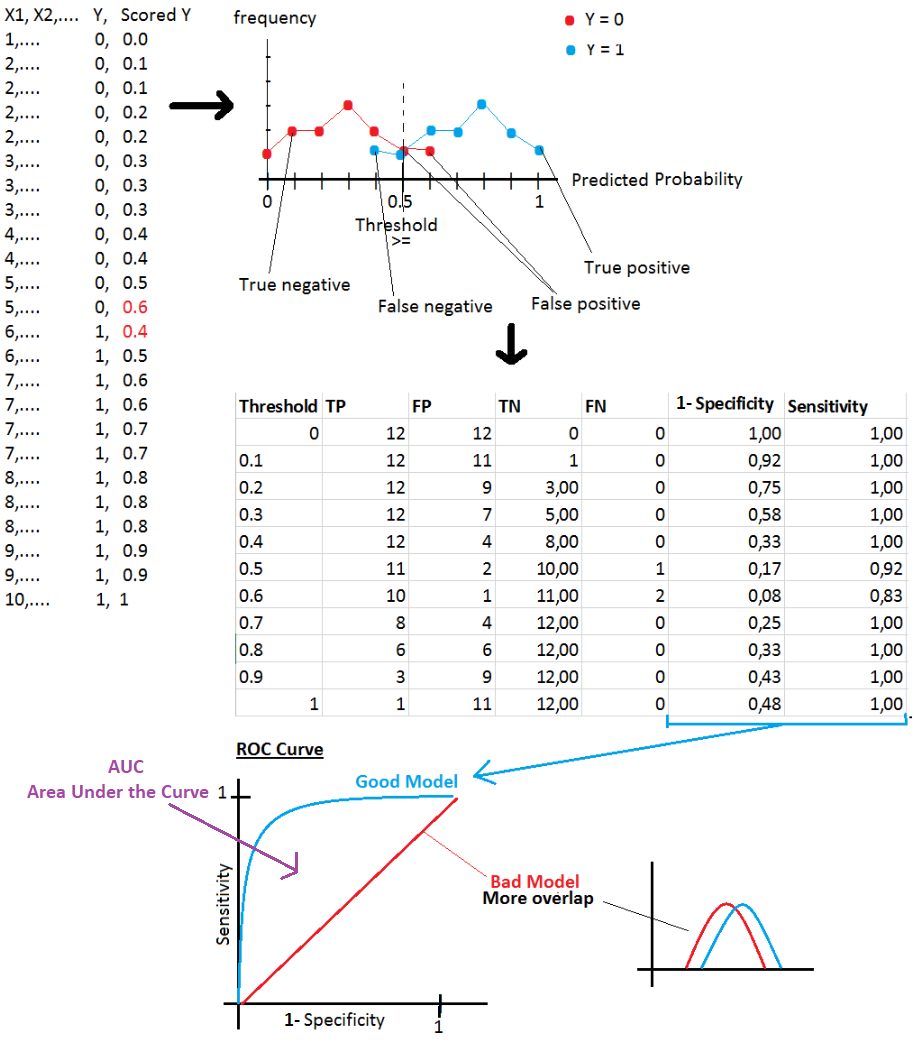
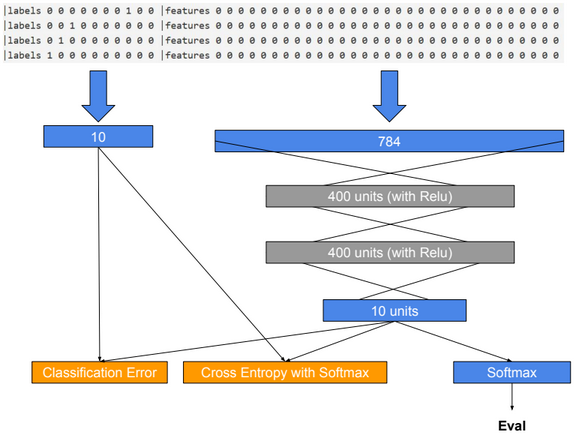
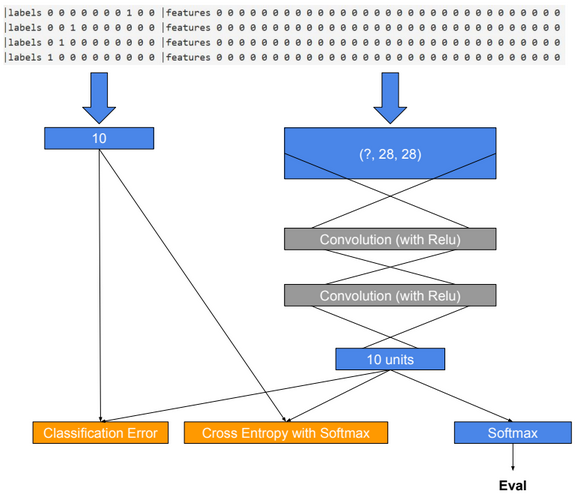
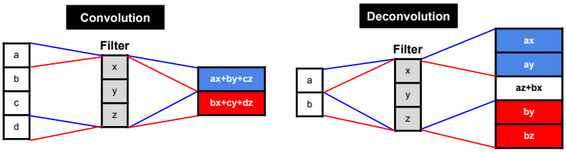
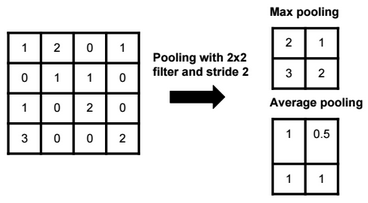
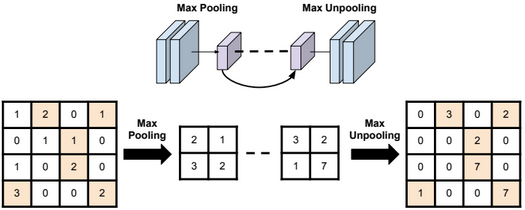
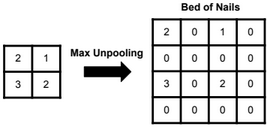
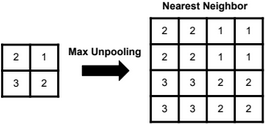
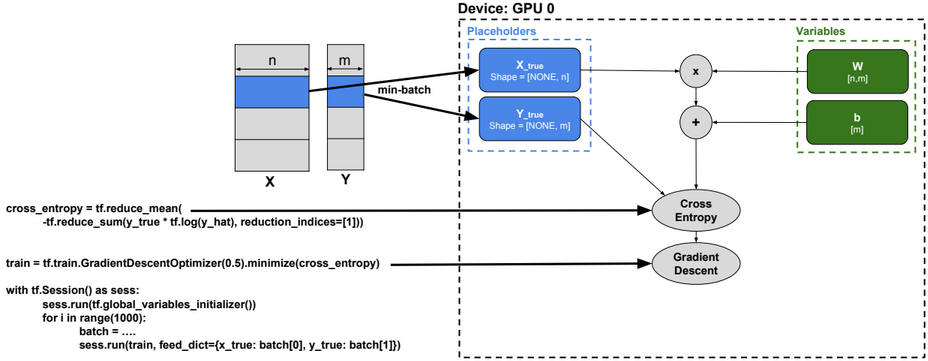
Dimensionality reduction is used to remove irrelevant and redundant features.
When the number of features in a dataset is bigger than the number of examples, then the probability density function of the dataset becomes difficult to calculate.
For example, if we model a dataset \(S = \{x^{(i)}\}_{i=1}^m,\ x \in R^{n}\) as a single Gaussian N(μ, ∑), then the probability density function is defined as: \(P(x) = \frac{1}{{(2π)}^{\frac{n}{2}} |Σ|^\frac{1}{2}} exp(-\frac{1}{2} (x-μ)^T {Σ}^{-1} (x-μ))\) such as \(μ = \frac{1}{m} \sum_{i=1}^m x^{(i)} \\ ∑ = \frac{1}{m} \sum_{i=1}^m (x^{(i)} – μ)(x^{(i)} – μ)^T\).
But If n >> m, then ∑ will be singular, and calculating P(x) will be impossible.
Note: \((x^{(i)} – μ)(x^{(i)} – μ)^T\) is always singular, but the \(\sum_{i=1}^m\) of many singular matrices is most likely invertible when m >> n.
Principal Component Analysis
Given a set \(S = \{x^{(1)}=(0,1), x^{(2)}=(1,1)\}\), to reduce the dimensionality of S from 2 to 1, we need to project data on a vector that maximizes the projections. In other words, find the normalized vector \(μ = (μ_1, μ_2)\) that maximizes \( ({x^{(1)}}^T.μ)^2 + ({x^{(2)}}^T.μ)^2 = (μ_2)^2 + (μ_1 + μ_2)^2\).
Using the method of Lagrange Multipliers, we can solve the maximization problem with constraint \(||u|| = μ_1^2 + μ_2^2 = 1\).
\(L(μ, λ) = (μ_2)^2 + (μ_1 + μ_2)^2 – λ (μ_1^2 + μ_2^2 – 1) \)We need to find μ such as \(∇_u = 0 \) and ||u|| = 1
After derivations we will find that the solution is the vector μ = (0.52, 0.85)
Generalization
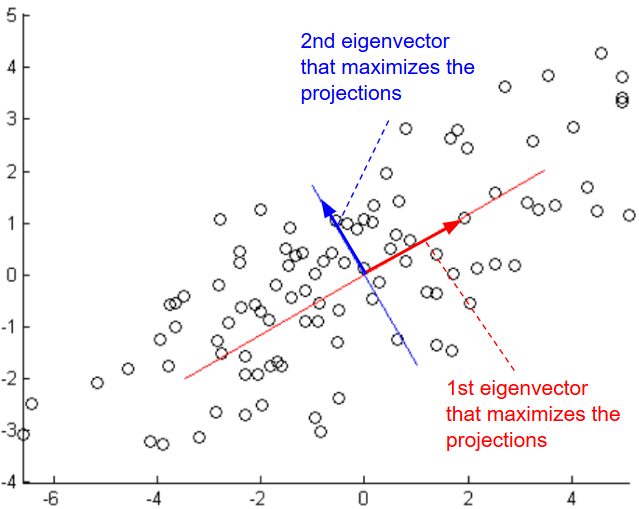
Given a set \(S = \{x^{(i)}\}_{i=1}^m,\ x \in R^{n}\), to reduce the dimensionality of S, we need to find μ that maximizes \(arg \ \underset{u: ||u|| = 1}{max} \frac{1}{m} \sum_{i=1}^m ({x^{(i)}}^T u)^2\)
\(=\frac{1}{m} \sum_{i=1}^m (u^T {x^{(i)}})({x^{(i)}}^T u)\) \(=u^T (\frac{1}{m} \sum_{i=1}^m {x^{(i)}} * {x^{(i)}}^T) u\)Let’s define \( ∑ = \frac{1}{m} \sum_{i=1}^m {x^{(i)}} * {x^{(i)}}^T \)
Using the method of Lagrange Multipliers, we can solve the maximization problem with constraint \(||u|| = u^Tu\) = 1.
\(L(μ, λ) = u^T ∑ u – λ (u^Tu – 1) \)If we calculate the derivative with respect to u, we will find:
\(∇_u = ∑ u – λ u = 0\)Therefore u that solves this maximization problem must be an eigenvector of ∑. We need to choose the eigenvector with highest eigenvalue.
If we choose k eigenvectors \({u_1, u_2, …, u_k}\), then we need to transform the data by multiplying each example with each eigenvector.
\(x^{(i)} := (u_1^T x^{(i)}, u_2^T x^{(i)},…, , u_k^T x^{(i)}) = U^T x^{(i)}\)Data should be normalized before running the PCA algorithm:
1-\(μ = \frac{1}{m} \sum_{i=1}^m x^{(i)}\)
2-\(x^{(i)} := x^{(i)} – μ\)
3-\(σ_j^{(i)} = \frac{1}{m} \sum_{i=1}^m {x_j^{(i)}}^2\)
4-\(x^{(i)} := \frac{x_j^{(i)}}{σ_j^{(i)}}\)
To reconstruct the original data, we need to calculate \(\widehat{x}^{(i)} := U^T x^{(i)}\)
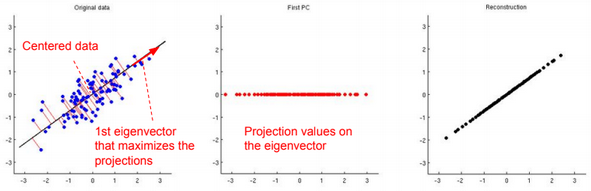
Factor Analysis
Factor analysis is a way to take a mass of data and shrinking it to a smaller data set with less features.
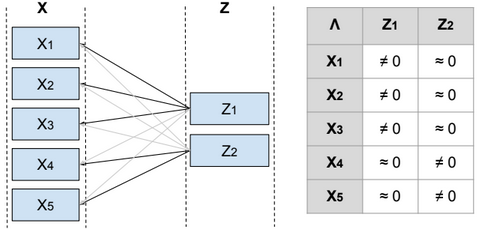
Given a set \(S = \{x^{(i)}\}_{i=1}^m,\ x \in R^{n}\), and S is modeled as a single Gaussian.
To reduce the dimensionality of S, we define a relationship between the variable x and a laten (hidden) variable z called factor such as \(x^{(i)} = μ + Λ z^{(i)} + ϵ^{(i)}\) and \(μ \in R^{n}\), \(z^{(i)} \in R^{d}\), \(Λ \in R^{n*d}\), \(ϵ \sim N(0, Ψ)\), Ψ is diagonal, \(z \sim N(0, I)\) and d <= n.
From Λ we can find the features that are related to each factor, and then identify the features that need to be eliminated or combined in order to reduce the dimensionality of the data.
Below the steps to estimate the parameters Ψ, μ, Λ.
\(E[x] = E[μ + Λz + ϵ] = E[μ] + ΛE[z] + E[ϵ] = μ \) \(Var(x) = E[(x – μ)^2] = E[(x – μ)(x – μ)^T] = E[(Λz + ϵ)(Λz + ϵ)^T]\) \(=E[Λzz^TΛ^T + ϵz^TΛ^T + Λzϵ^T + ϵϵ^T]\) \(=ΛE[zz^T]Λ^T + E[ϵz^TΛ^T] + E[Λzϵ^T] + E[ϵϵ^T]\) \(=Λ.Var(z).Λ^T + E[ϵz^TΛ^T] + E[Λzϵ^T] + Var(ϵ)\)ϵ and z are independent, then the join probability of p(ϵ,z) = p(ϵ)*p(z), and \(E[ϵz]=\int_{ϵ}\int_{z} ϵ*z*p(ϵ,z) dϵ dz\)
\(=\int_{ϵ}\int_{z} ϵ*z*p(ϵ)*p(z) dϵ dz\) \(=\int_{ϵ} ϵ*p(ϵ) \int_{z} z*p(z) dz dϵ\) \(=E[ϵ]E[z]\)So:
\(Var(x)=ΛΛ^T + Ψ\)Therefore \(x \sim N(μ, ΛΛ^T + Ψ)\) and \(P(x) = \frac{1}{{(2π)}^{\frac{n}{2}} |ΛΛ^T + Ψ|^\frac{1}{2}} exp(-\frac{1}{2} (x-μ)^T {(ΛΛ^T + Ψ)}^{-1} (x-μ))\)
\(Λ \in R^{n*d}\), if d <= m, then \(ΛΛ^T + Ψ\) is most likely invertible.
To find Ψ, μ, Λ, we need to maximize the log-likelihood function.
\(l(Ψ, μ, Λ) = \sum_{i=1}^m log(P(x^{(i)}; Ψ, μ, Λ))\) \(= \sum_{i=1}^m log(\frac{1}{{(2π)}^{\frac{n}{2}} |ΛΛ^T + Ψ|^\frac{1}{2}} exp(-\frac{1}{2} (x^{(i)}-μ)^T {(ΛΛ^T + Ψ)}^{-1} (x^{(i)}-μ)))\)This maximization problem cannot be solved by calculating the \(∇_Ψ l(Ψ, μ, Λ) = 0\), \(∇_μ l(Ψ, μ, Λ) = 0\), \(∇_Λ l(Ψ, μ, Λ) = 0\). However using the EM algorithm, we can solve that problem.
More details can be found in this video: https://www.youtube.com/watch?v=ey2PE5xi9-A
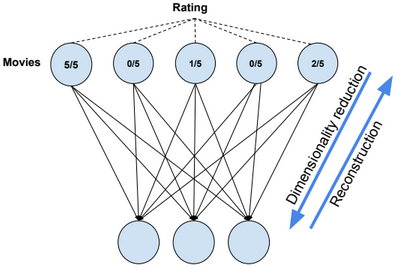
Restricted Boltzmann Machine
A restricted Boltzmann machine (RBM) is a two-layer stochastic neural network where the first layer consists of observed data variables (or visible units), and the second layer consists of latent variables (or hidden units). The visible layer is fully connected to the hidden layer. Both the visible and hidden layers are restricted to have no within-layer connections.
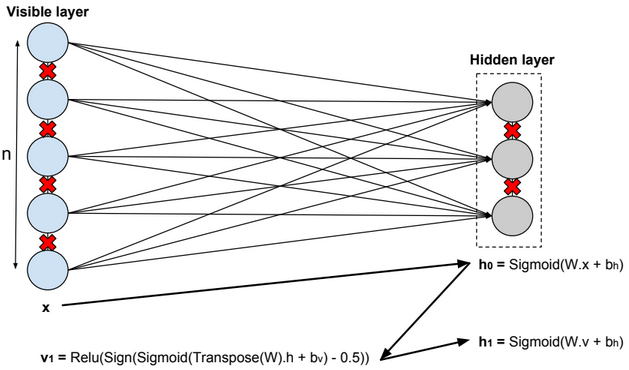
In this model, we update the parameters using the following equations:
\(W := W + α * \frac{x⊗Transpose(h_0) – v_1 ⊗ Transpose(h_1)}{n} \\ b_v := b_v + α * mean(x – v_1) \\ b_h := b_h + α * mean(h_0 – h_1) \\ error = mean(square(x – v_1))\).
Deep Belief Network
A deep belief network is obtained by stacking several RBMs on top of each other. The hidden layer of the RBM at layer i becomes the input of the RBM at layer i+1. The first layer RBM gets as input the input of the network, and the hidden layer of the last RBM represents the output.
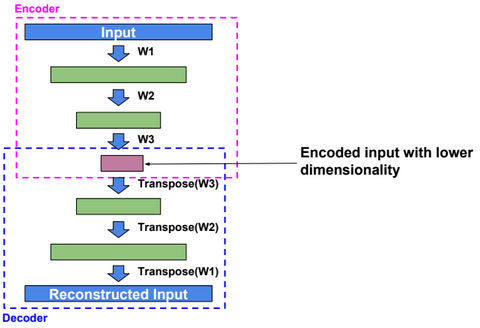
Autoencoders
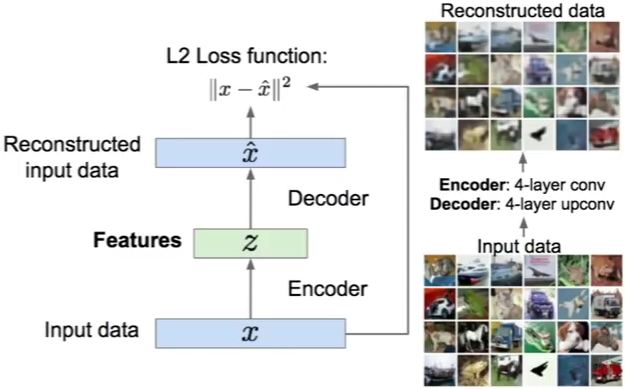
An autoencoder, autoassociator or Diabolo network is a deterministic artificial neural network used for unsupervised learning of efficient codings. The aim of an autoencoder is to learn a representation (encoding) for a set of data, typically for the purpose of dimensionality reduction. A deep Autoencoder contains multiple hidden units.
Loss function
For binary values, the loss function is defined as:
\(loss(x,\hat{x}) = -\sum_{k=1}^{size(x)} x_k.log(\hat{x_k}) + (1-x_k).log(1 – \hat{x_k})\).
For real values, the loss function is defined as:
\(loss(x,\hat{x}) = ½ \sum_{k=1}^{size(x)} (x_k – \hat{x_k})^2\).
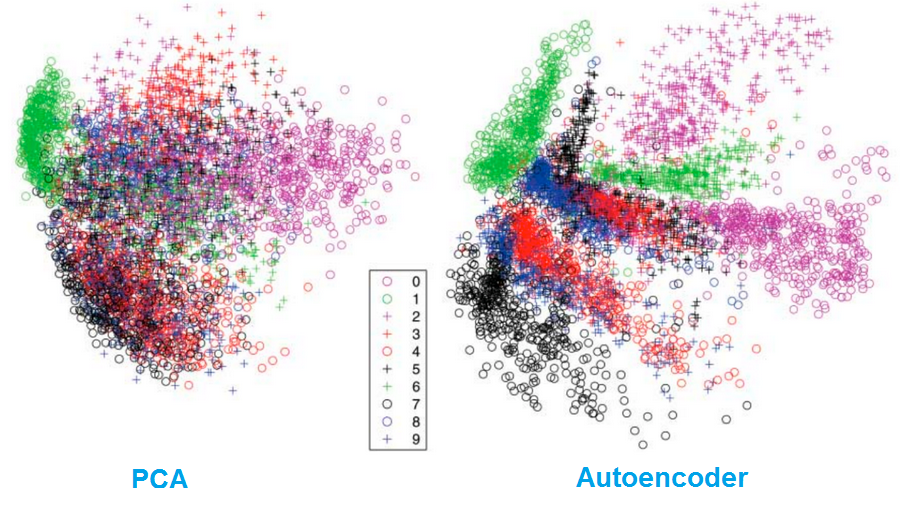
Dimensionality reduction
Autoencoders separate data better than PCA.
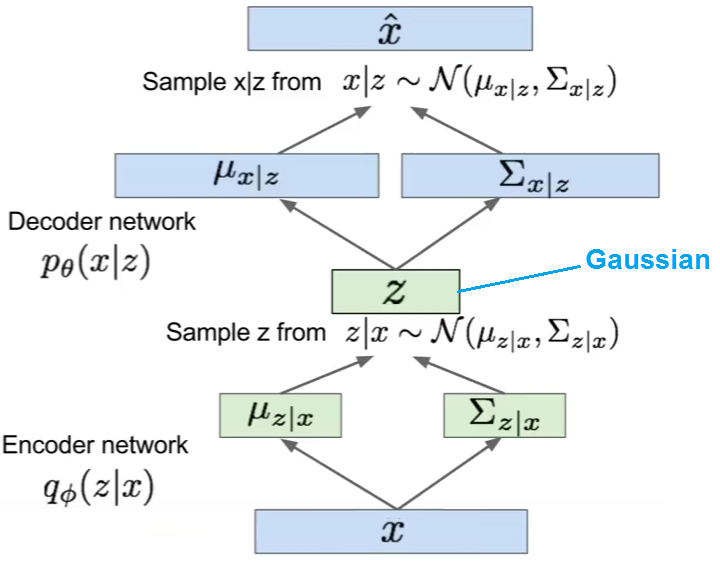
Variational Autoencoder
Variational autoencoder (VAE) models inherit autoencoder architecture, but make strong assumptions concerning the distribution of latent variables. In general, we suppose the distribution of the latent variable is gaussian.
The training algorithm used in VAEs is similar to EM algorithm.