by Sadek

Machine Learning Algorithms – Part 1

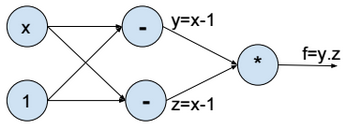
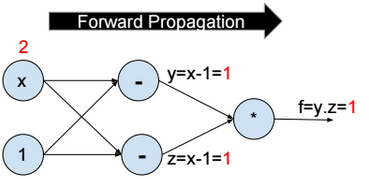
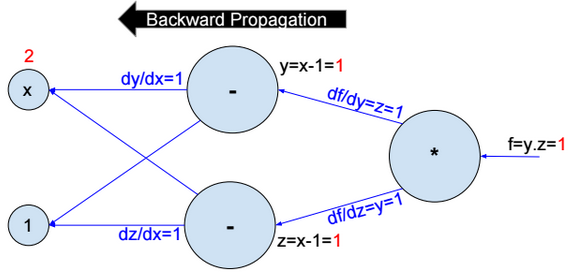
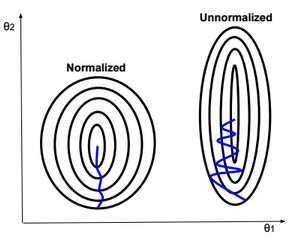
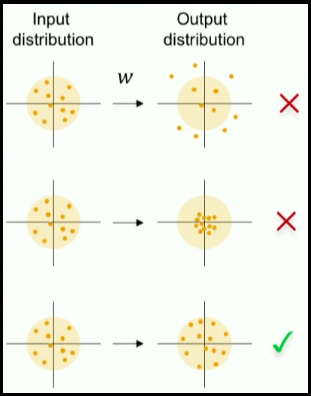
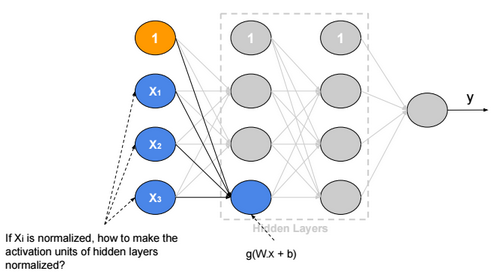
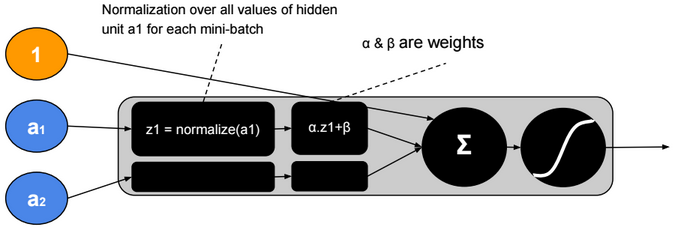
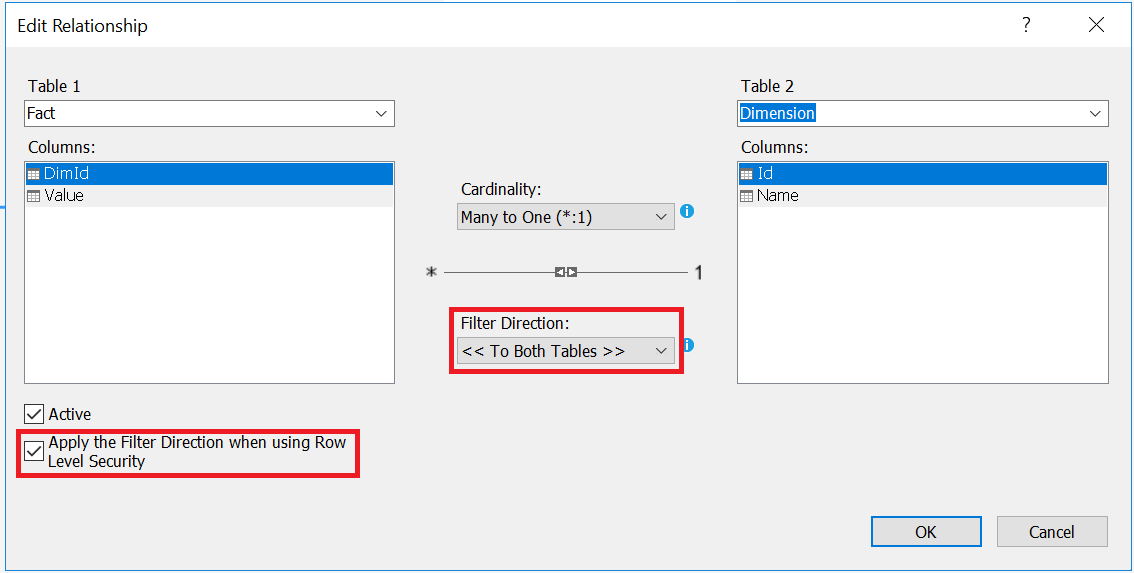
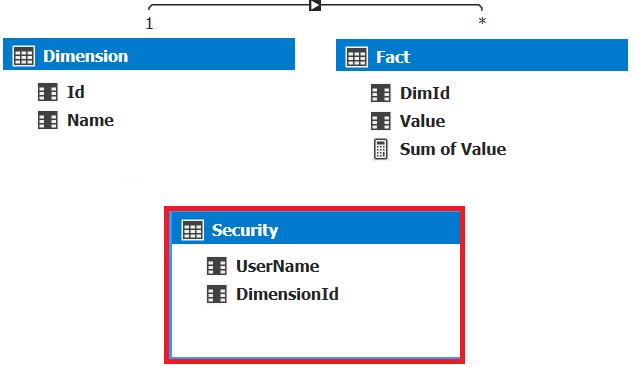
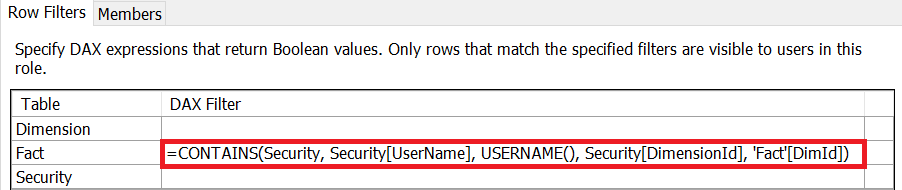
This post describes some discriminative machine learning algorithms.

Distribution of Y given X

Algorithm to predict Y

Normal distribution

Linear regression

Bernoulli distribution

Logistic regression

Multinomial distribution

Multinomial logistic regression (Softmax regression)

Exponential family distribution

Generalized linear regression

Distribution of X

Algorithm to predict Y

Multivariate normal distribution

Gaussian discriminant analysis or EM Algorithm

X Features conditionally independent

\(p(x_1, x_2|y)=p(x_1|y) * p(x_2|y) \)

Naive Bayes Algorithm

Other ML algorithms are based on geometry, like the SVM and K-means algorithms.

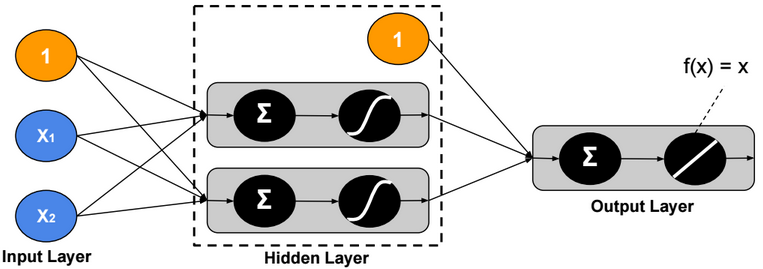
Linear Regression

Below a table listing house prices by size.

x = House Size (\(m^2\))

y = House Price (k$)

50

99

50

100

50

100

50

101

60

110

For the size 50\(m^2\), if we suppose that prices are normally distributed around the mean μ=100 with a standard deviation σ, then P(y|x = 50) = \(\frac{1}{\sigma \sqrt{2\pi}} exp(-\frac{1}{2} (\frac{y-μ}{\sigma})^{2})\)

We define h(x) as a function that returns the mean of the distribution of y given x (E[y|x]). We will define this function as a linear function. \(E[y|x] = h_{θ}(x) = \theta^T x\)

P(y|x = 50; θ) = \(\frac{1}{\sigma \sqrt{2\pi}} exp(-\frac{1}{2} (\frac{y-h_{θ}(x)}{\sigma})^{2})\)

We need to find θ that maximizes the probability for all values of x. In other words, we need to find θ that maximizes the likelihood function L:

\(L(\theta)=P(\overrightarrow{y}|X;θ)=\prod_{i=1}^{n} P(y^{(i)}|x^{(i)};θ)\)

Or maximizes the log likelihood function l:

\(l(\theta)=log(L(\theta )) = \sum_{i=1}^{m} log(P(y^{(i)}|x^{(i)};\theta ))\) \(= \sum_{i=1}^{m} log(\frac{1}{\sigma \sqrt{2\pi}}) -\frac{1}{2} \sum_{i=1}^{n} (\frac{y^{(i)}-h_{θ}(x^{(i)})}{\sigma})^{2}\)

To maximize l, we need to minimize J(θ) = \(\frac{1}{2} \sum_{i=1}^{m} (y^{(i)}-h_{θ}(x^{(i)}))^{2}\). This function is called the Cost function (or Energy function, or Loss function, or Objective function) of a linear regression model. It’s also called “Least-squares cost function”.

J(θ) is convex, to minimize it, we need to solve the equation \(\frac{\partial J(θ)}{\partial θ} = 0\). A convex function has no local minimum.

There are many methods to solve this equation:

  • Gradient descent (Batch or Stochastic Gradient descent)
  • Normal equation
  • Newton method
  • Matrix differentiation

Gradient descent is the most used Optimizer (also called Learner or Solver) for learning model weights.

Batch Gradient descent

\(θ_{j} := θ_{j} – \alpha \frac{\partial J(θ)}{\partial θ_{j}} = θ_{j} – α \frac{\partial \frac{1}{2} \sum_{i=1}^{n} (y^{(i)}-h_{θ}(x^{(i)}))^{2}}{\partial θ_{j}}\)

α is called “Learning rate”

\(θ_{j} := θ_{j} – α \frac{1}{2} \sum_{i=1}^{n} \frac{\partial (y^{(i)}-h_{θ}(x^{(i)}))^{2}}{\partial θ_{j}}\)

If \(h_{θ}(x)\) is a linear function (\(h_{θ} = θ^{T}x\)), then :

\(θ_{j} := θ_{j} – α \sum_{i=1}^{n} (h_{θ}(x^{(i)}) – y^{(i)}) * x_j^{(i)} \)

Batch size should fit the size of CPU or GPU memories, otherwise learning speed will be extremely slow.

When using Batch gradient descent, the cost function in general decreases without oscillations.

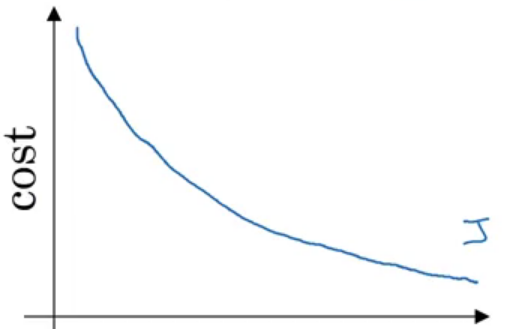
Stochastic (Online) Gradient Descent (SGD) (use one example for each iteration – pass through all data N times (N Epoch))

\(θ_{j} := θ_{j} – \alpha (h_{θ}(x^{(i)}) – y^{(i)}) * x_j^{(i)} \)

This learning rule is called “Least mean squares (LMS)” learning rule. It’s also called Widrow-Hoff learning rule.

Mini-batch Gradient descent

Run gradient descent for each mini-batch until we pass through traning set (1 epoch). Repeat the operation many times.

\(θ_{j} := θ_{j} – \alpha \sum_{i=1}^{20} (h_{θ}(x^{(i)}) – y^{(i)}) * x_j^{(i)} \)

Mini-batch size should fit the size of CPU or GPU memories.

When using Batch gradient descent, the cost function decreases quickly but with oscillations.

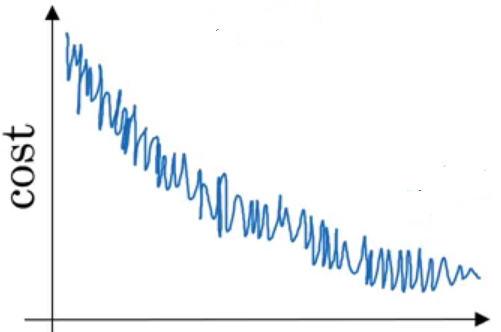
Learning rate decay

It’s a technique used to automatically reduce learning rate after each epoch. Decay rate is a hyperparameter.

\(α = \frac{1}{1+ decayrate + epochnum} . α_0\)

Momentum

Momentum is a method used to accelerate gradient descent. The idea is to add an extra term to the equation to accelerate descent steps.

\(θ_{j_{t+1}} := θ_{j_t} – α \frac{\partial J(θ_{j_t})}{\partial θ_j} \color{blue} {+ λ (θ_{j_t} – θ_{j_{t-1}})} \)

Below another way to write the expression:

\(v(θ_{j},t) = α . \frac{\partial J(θ_j)}{\partial θ_j} + λ . v(θ_{j},t-1) \\ θ_{j} := θ_{j} – \color{blue} {v(θ_{j},t)}\)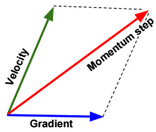

Nesterov Momentum is a slightly different version of momentum method.

AdaGrad

Adam is another method used to accelerate gradient descent.

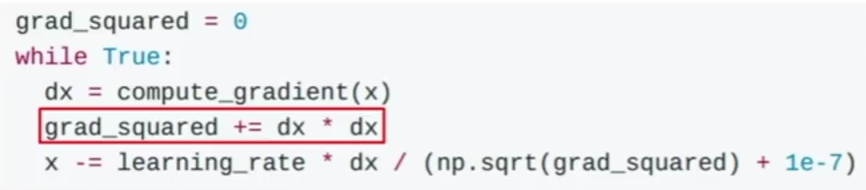
The problem in this method is that the term grad_squared becomes large after running many gradient descent steps. The term grad_squared is used to accelerate gradient descent when gradients are small, and slow down gradient descent when gradients are large.

RMSprop

RMSprop is an enhanced version of AdaGrad.

The term decay_rate is used to apply exponential smoothing on grad_squared term.

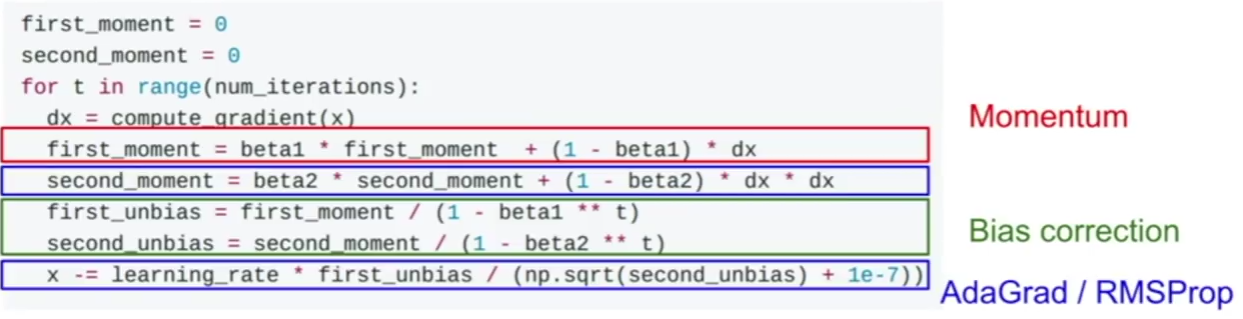
Adam optimization

Adam is a combination of Momentum and RMSprop.

Normal equation

To minimize the cost function \(J(θ) = \frac{1}{2} \sum_{i=1}^{n} (y^{(i)}-h_{θ}(x^{(i)}))^{2} = \frac{1}{2} (Xθ – y)^T(Xθ – y)\), we need to solve the equation:

\( \frac{\partial J(θ)}{\partial θ} = 0 \\ \frac{\partial trace(J(θ))}{\partial θ} = 0 \\ \frac{\partial trace((Xθ – y)^T(Xθ – y))}{\partial θ} = 0 \\ \frac{\partial trace(θ^TX^TXθ – θ^TX^Ty – y^TXθ + y^Ty)}{\partial θ} = 0\) \(\frac{\partial trace(θ^TX^TXθ) – trace(θ^TX^Ty) – trace(y^TXθ) + trace(y^Ty))}{\partial θ} = 0 \\ \frac{\partial trace(θ^TX^TXθ) – trace(θ^TX^Ty) – trace(y^TXθ))}{\partial θ} = 0\) \(\frac{\partial trace(θ^TX^TXθ) – trace(y^TXθ) – trace(y^TXθ))}{\partial θ} = 0 \\ \frac{\partial trace(θ^TX^TXθ) – 2 trace(y^TXθ))}{\partial θ} = 0 \\ \frac{\partial trace(θθ^TX^TX)}{\partial θ} – 2 \frac{\partial trace(θy^TX))}{\partial θ} = 0 \\ 2 X^TXθ – 2 X^Ty = 0 \\ X^TXθ= X^Ty \\ θ = {(X^TX)}^{-1}X^Ty\)

If \(X^TX\) is singular, then we need to calculate the pseudo inverse instead of the inverse.

Newton method

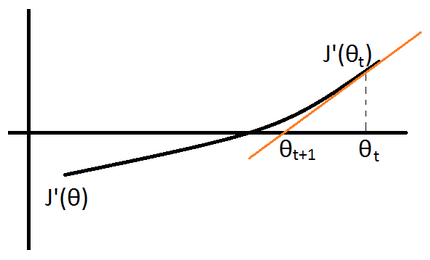
\(J”(θ_{t}) := \frac{J'(θ_{t+1}) – J'(θ_{t})}{θ_{t+1} – θ_{t}}\) \(\rightarrow θ_{t+1} := θ_{t} – \frac{J'(θ_{t})}{J”(θ_{t})}\)

Matrix differentiation

To minimize the cost function: \(J(θ) = \frac{1}{2} \sum_{i=1}^{n} (y^{(i)}-h_{θ}(x^{(i)}))^{2} = \frac{1}{2} (Xθ – y)^T(Xθ – y)\), we need to solve the equation:

\( \frac{\partial J(θ)}{\partial θ} = 0 \\ \frac{\partial θ^TX^TXθ – θ^TX^Ty – y^TXθ + y^Ty}{\partial θ} = 2X^TXθ – \frac{\partial θ^TX^Ty}{\partial θ} – X^Ty = 0\)

\(2X^TXθ – \frac{\partial y^TXθ}{\partial θ} – X^Ty = 2X^TXθ – 2X^Ty = 0\) (Note: In matrix differentiation: \( \frac{\partial Aθ}{\partial θ} = A^T\) and \( \frac{\partial θ^TAθ}{\partial θ} = 2A^Tθ\))

we can deduce \(X^TXθ = X^Ty\) and \(θ = (X^TX)^{-1}X^Ty\)

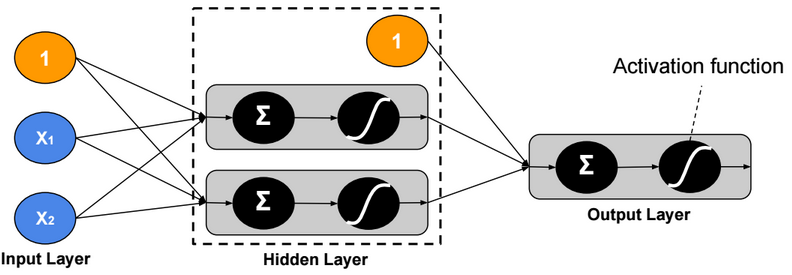
Logistic Regression

Below a table that shows tumor types by size.

x = Tumor Size (cm)

y = Tumor Type (Benign=0, Malignant=1)

1

0

1

0

2

0

2

1

3

1

3

1

Given x, y is distributed according to the Bernoulli distribution with probability of success p = E[y|x].

\(P(y|x;θ) = p^y (1-p)^{(1-y)}\)

We define h(x) as a function that returns the expected value (p) of the distribution. We will define this function as:

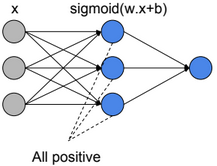
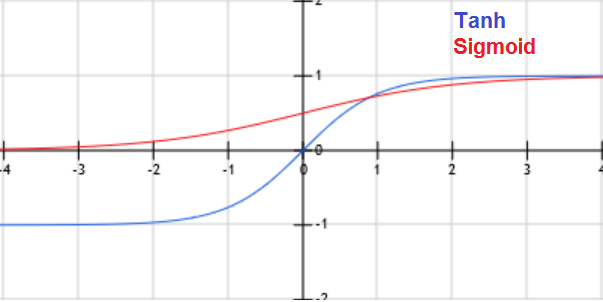
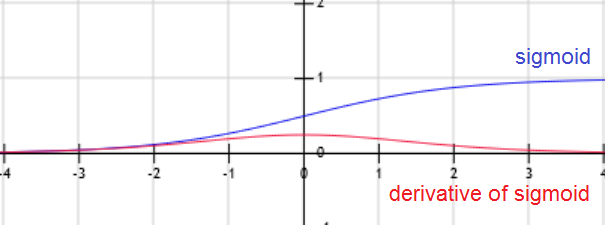
\(E[y|x] = h_{θ}(x) = g(θ^T x) = \frac{1}{1+exp(-θ^T x)}\). g is called Sigmoid (or logistic) function.

P(y|x; θ) = \(h_{θ}(x)^y (1-h_{θ}(x))^{(1-y)}\)

We need to find θ that maximizes this probability for all values of x. In other words, we need to find θ that maximizes the likelihood function L:

\(L(θ)=P(\overrightarrow{y}|X;θ)=\prod_{i=1}^{m} P(y^{(i)}|x^{(i)};θ)\)

Or maximize the log likelihood function l:

\(l(θ)=log(L(θ)) = \sum_{i=1}^{m} log(P(y^{(i)}|x^{(i)};θ ))\) \(= \sum_{i=1}^{m} y^{(i)} log(h_{θ}(x^{(i)}))+ (1-y^{(i)}) log(1-h_{θ}(x^{(i)}))\)

Or minimize the \(-l(θ) = \sum_{i=1}^{m} -y^{(i)} log(h_{θ}(x^{(i)})) – (1-y^{(i)}) log(1-h_{θ}(x^{(i)})) = J(θ) \)

J(θ) is convex, to minimize it, we need to solve the equation \(\frac{\partial J(θ)}{\partial θ} = 0\).

There are many methods to solve this equation:

  • Gradient descent

Gradient descent

\(θ_{j} := θ_{j} – α \sum_{i=1}^{n} (h_{θ}(x^{(i)}) – y^{(i)}) * x_j^{(i)} \)

Logit function (inverse of logistic function)

Logit function is defined as follow: \(logit(p) = log(\frac{p}{1-p})\)

The idea in the use of this function is to transform the interval of p (outcome) from [0,1] to [0, ∞]. So instead of applying linear regression on p, we will apply it on logit(p).

Once we find θ that maximizes the Likelihood function, we can then estimate logit(p) given a value of x (\(logit(p) = h_{θ}(x) \)). p can be then calculated using the following formula:

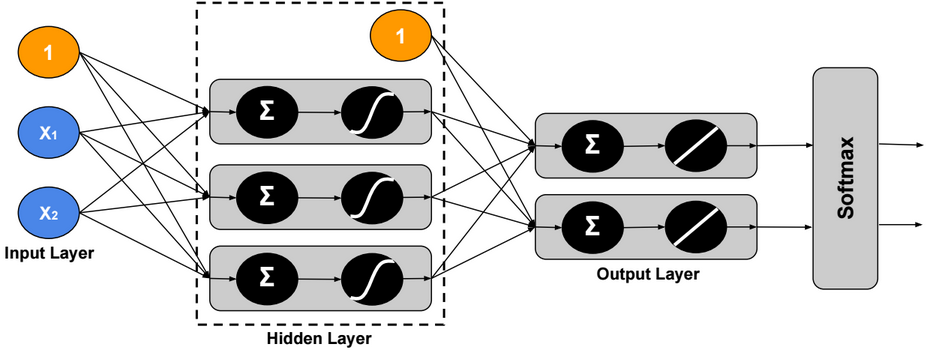
\(p = \frac{1}{1+exp(-logit(h_{θ}(x)))}\)

Multinomial Logistic Regression (using maximum likelihood estimation)

In multinomial logistic regression (also called Softmax Regression), y could have more than two outcomes {1,2,3,…,k}.

Below a table that shows tumor types by size.

x = Tumor Size (cm)

y = Tumor Type (Type1= 1, Type2= 2, Type3= 3)

1

1

1

1

2

2

2

2

2

3

3

3

3

3

Given x, we can define a multinomial distribution with probabilities of success \(\phi_j = E[y=j|x]\).

\(P(y=j|x;\Theta) = ϕ_j \\ P(y=k|x;\Theta) = 1 – \sum_{j=1}^{k-1} ϕ_j \\ P(y|x;\Theta) = ϕ_1^{1\{y=1\}} * … * ϕ_{k-1}^{1\{y=k-1\}} * (1 – \sum_{j=1}^{k-1} ϕ_j)^{1\{y=k\}}\)

We define \(\tau(y)\) as a function that returns a \(R^{k-1}\) vector with value 1 at the index y: \(\tau(y) = \begin{bmatrix}0\\0\\1\\0\\0\end{bmatrix}\), when \(y \in \{1,2,…,k-1\}\), .

and \(\tau(y) = \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}\), when y = k.

We define \(\eta(x)\) as a \(R^{k-1}\) vector = \(\begin{bmatrix}log(\phi_1/\phi_k)\\log(\phi_2/\phi_k)\\…\\log(\phi_{k-1}/\phi_k)\end{bmatrix}\)

\(P(y|x;\Theta) = 1 * exp(η(x)^T * \tau(y) – (-log(\phi_k)))\)

This form is an exponential family distribution form.

We can invert \(\eta(x)\) and find that:

\(ϕ_j = ϕ_k * exp(η(x)_j)\) \(= \frac{1}{1 + \frac{1-ϕ_k}{ϕ_k}} * exp(η(x)_j)\) \(=\frac{exp(η(x)_j)}{1 + \sum_{c=1}^{k-1} ϕ_c/ϕ_k}\) \(=\frac{exp(η(x)_j)}{1 + \sum_{c=1}^{k-1} exp(η(x)_c)}\)

If we define η(x) as linear function, \(η(x) = Θ^T x = \begin{bmatrix}Θ_{1,1} x_1 +… + Θ_{n,1} x_n \\Θ_{1,2} x_1 +… + Θ_{n,2} x_n\\…\\Θ_{1,k-1} x_1 +… + Θ_{n,k-1} x_n\end{bmatrix}\), and Θ is a \(R^{n*(k-1)}\) matrix.

Then: \(ϕ_j = \frac{exp(Θ_j^T x)}{1 + \sum_{c=1}^{k-1} exp(Θ_c^T x)}\)

The hypothesis function could be defined as: \(h_Θ(x) = \begin{bmatrix}\frac{exp(Θ_1^T x)}{1 + \sum_{c=1}^{k-1} exp(Θ_c^T x)} \\…\\ \frac{exp(Θ_{k-1}^T x)}{1 + \sum_{c=1}^{k-1} exp(Θ_c^T x)} \end{bmatrix}\)

We need to find Θ that maximizes the probabilities P(y=j|x;Θ) for all values of x. In other words, we need to find θ that maximizes the likelihood function L:

\(L(θ)=P(\overrightarrow{y}|X;θ)=\prod_{i=1}^{m} P(y^{(i)}|x^{(i)};θ)\) \(=\prod_{i=1}^{m} \phi_1^{1\{y^{(i)}=1\}} * … * \phi_{k-1}^{1\{y^{(i)}=k-1\}} * (1 – \sum_{j=1}^{k-1} \phi_j)^{1\{y^{(i)}=k\}}\) \(=\prod_{i=1}^{m} \prod_{c=1}^{k-1} \phi_c^{1\{y^{(i)}=c\}} * (1 – \sum_{j=1}^{k-1} \phi_j)^{1\{y^{(i)}=k\}}\)

\(=\prod_{i=1}^{m} \prod_{c=1}^{k-1} \phi_c^{1\{y^{(i)}=c\}} * (1 – \sum_{j=1}^{k-1} \phi_j)^{1\{y^{(i)}=k\}}\) and \(ϕ_j = \frac{exp(Θ_j^T x)}{1 + \sum_{c=1}^{k-1} exp(Θ_c^T x)}\)

Multinomial Logistic Regression (using cross-entropy minimization)

In this section, we will try to minimize the cross-entropy between Y and estimated \(\widehat{Y}\).

We define \(W \in R^{d*n}\), \(b \in R^{d}\) such as \(S(W x + b) = \widehat{Y}\), S is the Softmax function, k is the number of outputs, and \(x \in R^n\).

To estimate W and b, we will need to minimize the cross-entropy between the two probability vectors Y and \(\widehat{Y}\).

The cross-entropy is defined as below:

\(D(\widehat{Y}, Y) = -\sum_{j=1}^d Y_j Log(\widehat{Y_j})\)

Example:

if \(\widehat{y} = \begin{bmatrix}0.7 \\0.1 \\0.2 \end{bmatrix} \& \ y=\begin{bmatrix}1 \\0 \\0 \end{bmatrix}\) then \(D(\widehat{Y}, Y) = D(S(W x + b), Y) = -1*log(0.7)\)

We need to minimize the entropy for all training examples, therefore we will need to minimize the average cross-entropy of the entire training set.

\(L(W,b) = \frac{1}{m} \sum_{i=1}^m D(S(W x^{(i)} + b), y^{(i)})\), L is called the loss function.

If we define \(W = \begin{bmatrix} — θ_1 — \\ — θ_2 — \\ .. \\ — θ_d –\end{bmatrix}\) such as:

\(θ_1=\begin{bmatrix}θ_{1,0}\\θ_{1,1}\\…\\θ_{1,n}\end{bmatrix}, θ_2=\begin{bmatrix}θ_{2,0}\\θ_{2,1}\\…\\θ_{2,n}\end{bmatrix}, θ_d=\begin{bmatrix}θ_{d,0}\\θ_{d,1}\\…\\θ_{d,n}\end{bmatrix}\)

We can then write \(L(W,b) = \frac{1}{m} \sum_{i=1}^m D(S(W x^{(i)} + b), y^{(i)})\)

\(= \frac{1}{m} \sum_{i=1}^m \sum_{j=1}^d 1^{\{y^{(i)}=j\}} log(\frac{exp(θ_k^T x^{(i)})}{\sum_{k=1}^d exp(θ_k^T x^{(i)})})\)

For d=2 (nbr of class=2), \(= \frac{1}{m} \sum_{i=1}^m 1^{\{y^{(i)}=\begin{bmatrix}1 \\ 0\end{bmatrix}\}} log(\frac{exp(θ_1^T x^{(i)})}{exp(θ_1^T x^{(i)}) + exp(θ_2^T x^{(j)})}) + 1^{\{y^{(i)}=\begin{bmatrix}0 \\ 1\end{bmatrix}\}} log(\frac{exp(θ_2^T x^{(i)})}{exp(θ_1^T x^{(i)}) + exp(θ_2^T x^{(i)})})\)

\(1^{\{y^{(i)}=\begin{bmatrix}1 \\ 0\end{bmatrix}\}}\) means that the value is 1 if \(y^{(i)}=\begin{bmatrix}1 \\ 0\end{bmatrix}\) otherwise the value is 0.

To estimate \(θ_1,…,θ_d\), we need to calculate the derivative and update \(θ_j = θ_j – α \frac{\partial L}{\partial θ_j}\)

Kernel regression

Kernel regression is a non-linear model. In this model we define the hypothesis as the sum of kernels.

\(\widehat{y}(x) = ϕ(x) * θ = θ_0 + \sum_{i=1}^d K(x, μ_i, λ) θ_i \) such as:

\(ϕ(x) = [1, K(x, μ_1, λ),…, K(x, μ_d, λ)]\) and \(θ = [θ_0, θ_1,…, θ_d]\)

For example, we can define the kernel function as : \(K(x, μ_i, λ) = exp(-\frac{1}{λ} ||x-μ_i||^2)\)

Usually we select d = number of training examples, and \(μ_i = x_i\)

Once the vector ϕ(X) calculated, we can use it as new engineered vector, and then use the normal equation to find θ:

\(θ = {(ϕ(X)^Tϕ(X))}^{-1}ϕ(X)^Ty\)

Bayes Point Machine

The Bayes Point Machine is a Bayesian linear classifier that can be converted to a nonlinear classifier by using feature expansions or kernel methods as the Support Vector Machine (SVM).

More details will be provided.

Ordinal Regression

Ordinal Regression is used for predicting an ordinal variable. An ordinal variable is a categorical variable for which the possible values are ordered (eg. size: Small, Medium, Large).

More details will be provided.

Poisson Regression

Poisson regression assumes the output variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear function.

log(E[Y|X]) = log(λ) = θ.x

by Sadek

Feature Engineering

Hashing

Feature hashing is used to convert a categorical feature into a small-dimension feature space.

For example a vocabulary of words can be represented in a 5 dimensional space \(\{0,1\}^5\) (e.g. Apple → [1,0,1,1,0]).

Hashing introduces noise as collisions are permitted (Car→ [0,0,0,1,1], Flight→ [0,0,0,1,1]).

Embedding

With embedding the representation is more dense (e.g. Car → [0.4,0.9,0.1,0,0.1])

Bucketing

Bucketing is a technique for decomposing feature values into buckets.

Crossing

Crossing features is combining multiple features in one feature.

by Sadek

Recurrent Neural Network

Architecture

RNNs are generally used for sequence modeling (e.g. language modeling, time series modeling,…).

Unfolding a RNN network (many to many scenario) could be presented as follow:

When training the model, we need to find W that minimizes the sum of losses.

Multilayer RNN

Multilayer RNN is a neural network with multiple RNN layers.

Backpropagation through time

To train a RNN, we need to calculate the gradient to update parameters. Instead of doing the derivations for the full network, we will focus only on one hidden unit.

We define \(s_t = g(W.x_t + U.s_{t-1} + b) \). g is an activation function.

Using the chain rule we can find that:

\(\frac{\partial loss(y_t,?_t)}{\partial W} = \frac{\partial loss(y_t,?_t)}{\partial ?_t}.\frac{\partial ?_t}{\partial s_t}.\frac{\partial s_t}{\partial W} \\ = \frac{\partial loss(y_t,?_t)}{\partial ?_t}.\frac{\partial ?_t}{\partial s_t}.(\sum_{k=t}^0 \frac{\partial s_t}{\partial s_k}.\frac{\partial s_k}{\partial W})\)

Vanishing gradient

The term in red in the equation is a product of Jacobians (\(\frac{\partial s_t}{\partial s_k} = \prod_{i=k+1}^{t} \frac{\partial s_{i}}{\partial s_{i-1}}\)).

\(\frac{\partial loss(y_t,?_t)}{\partial ?_t}.\frac{\partial ?_t}{\partial s_t}.(\sum_{k=t}^0 \color{red} {\frac{\partial s_t}{\partial s_k}}.\frac{\partial s_k}{\partial W})\)

Because the derivatives of activation functions (except ReLU) are less than 1, therefore when evaluating the gradient, the red term tends to converge to 0, and the model becomes more biased and captures less dependencies.

Exploding gradient

RNN is trained by backpropagation through time. When gradient is passed back through many time steps, it tends to vanish or to explode.

Gradient Clipping

Gradient Clipping is a technique to prevent exploding gradients in very deep networks, typically Recurrent Neural Networks. There are various ways to perform gradient clipping, but the most common one is to normalize the gradients of a parameter vector when its L2 norm exceeds a certain threshold according to : \(gradients := gradients * \frac{threshold}{L2 norm(gradients)}\).

Long Short Term Memory (LSTM)

LSTM was introduced to solve the vanishing gradient problem.

In LSTM, there are 4 gates that regulate the state of a RNN model:

Write gate (i?[0,1]) (Input gate): Write to memory cell.

Keep gate (f?[0,1]) (Forget gate): Erase memory cell.

Read gate (o?[0,1]) (Output gate): Read from memory cell.

Gate gate (g?[-1,1]) (Update gate) How much to write to memory cell.

\(c_t\) is called memory state at time t.

i,f,o,g,h,c are vectors having the same size. W is a matrix with size nxh.

The gate states are calculated using the following formula:

The output \(h_t\) is calculated using the following formulas:

\(c_t = f.c_{t-1} + i.g \\ h_t = o.tanh(c_t)\)

Gated Recurrent Unit (GRU)

The Gated Recurrent Unit is a simplified version of an LSTM unit with fewer parameters. Just like an LSTM cell, it uses a gating mechanism to allow RNNs to efficiently learn long-range dependency by preventing the vanishing gradient problem. The GRU consists of a reset and update gates that determine which part of the old memory to keep or update with new values at the current time step.

by Sadek

Introduction to Quantum Computing

I think I can safely say that nobody understands quantum mechanics. ~ Richard Feynman.

Hilbert space

Hilbert space is generalization of the Euclidean space. In a Hilbert space we can have infinite number of dimensions.

A vector in an infinite-dimensional Hilbert space is represented as an infinite vector: \((x_1, x_2, .)\).

The inner product of two vectors \(?x|y? = \sum_{i=1}^? x_i y_i\)

The norm \( ||x|| = ?x|x?^{\frac{1}{2}} = \sqrt{\sum_{i=1}^? x_i^2} < ?\)

Tensor product of two vectors \(\begin{bmatrix} a_1 \\ a_2 \end{bmatrix} ? \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} a_1 * b_1 \\ a_1 * b_2 \\ a_2 * b_1 \\ a_2 * b_2 \end{bmatrix}\)

Qubit

In quantum computing, a qubit or quantum bit is a unit of quantum information. Its the analog of a bit for quantum computation. A qubit is a two-state quantum-mechanical system. The state 0 could be represented as vector \(\begin{bmatrix} 1 \\ 0 \end{bmatrix} ? |0? ? |??\) (horizontal polarization) and state 1 could be represented as orthogonal vector \(\begin{bmatrix} 0 \\ 1 \end{bmatrix} ? |1? ? |??\) (vertical polarization) .

A generic qubit state corresponds to a vector \(\begin{bmatrix} ? \\ ? \end{bmatrix} = ? \begin{bmatrix} 1 \\ 0 \end{bmatrix} + ? \begin{bmatrix} 0 \\ 1 \end{bmatrix} ? ? \ |0? + ? \ |1? \) in a two-dimensional Hilbert space such as \(|?|^2 + |?|^2 = 1\) (normalized vector). \(|?|^2, |?|^2\) are the probabilities for the particle to be in state 0 and 1. ? and ? are complex numbers and they are called amplitudes.

Another way to write the state ? of a qubit is by using cos and sin functions.

|?? = cos(?) |0? + sin(?) |1?

More details about qubit can be found here: https://arxiv.org/pdf/1312.1463.pdf

Two qubits

A state in a combined two qubits system corresponds to a vector in four-dimensional Hilbert space \(|\gamma? = e \ |00? + f \ |01? + g \ |10?+ h \ |11? = \begin{bmatrix} e \\ f \\ g \\ h \end{bmatrix} \).

In general, the state vector of two combined systems is the tensor product of the state vector of each system.

Some expressions and their equivalents:

|0??|0??|0? ? |000?

|0??|1??|0? ? |010?

\((\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?)?(\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?) ? \frac{1}{2}|00? + \frac{1}{2}|01? + \frac{1}{2}|10? + \frac{1}{2}|11?\)

Bloch sphere

A state ? of a qubit can be also written as: \(|?? = cos(\frac{?}{2})|0? + sin(\frac{?}{2}) exp(i?) |1?\), and it can be visualized as a vector of length 1 on the Bloch sphere.

The angles ?,? correspond to the polar and azimuthal angles of spherical coordinates (??[0,?], ??[0,2?]).

Bra-ket notation

|01? ? |0??|1? ? \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \) (column vector)

?01| ? ?0|??1| ? \(\begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix} \) (row vector)

Quantum superposition

An arbitrary state of a qubit could be described as a superposition of 0 and 1 states.

N qubits

A 3 qubits quantum system can store numbers such as 3 or 7.

|011? ? |3?

|111? ? |7?

But it can also store the two numbers simultaneously using a superposition state on the last qubit.

\((\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?)?|1??|1? ? \sqrt{\frac{1}{2}} (|011? + |111?)\)

In general, a quantum computer with n qubits can be in an arbitrary superposition of up to \(2^n\) different states simultaneously.

Quantum gates

Hadamard H gate

The Hadamard gate acts on a single qubit. It maps the state |0? to a superposition state with equal probabilities on state 0 and 1 (\(\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?\)).

The Hadamard matrix is defined as: \(H = \frac {1}{\sqrt {2}} \begin{bmatrix}1 \ 1 \\ 1 \ -1 \end{bmatrix}\)

\(H * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \sqrt{\frac{1}{2}} \\ \sqrt{\frac{1}{2}} \end{bmatrix}\)

Pauli X gate (NOT gate)

The Pauli-X gate acts on a single qubit. It is the quantum equivalent of the NOT gate for classical computers.

The Pauli X matrix is defined as: \(X = \begin{bmatrix}0 \ 1 \\ 1 \ 0 \end{bmatrix}\)

\(X * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)

Pauli Y gate

The Pauli-Y gate acts on a single qubit. It equates to a rotation around the Y-axis of the Bloch sphere by ? radians. It maps |0? to i |1? and |1? to ?i |0?

The Pauli Y matrix is defined as: \(Y = \begin{bmatrix}0 \ -i \\ i \ 0 \end{bmatrix}\)

\(Y * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ i \end{bmatrix}\)

Pauli Z gate

The Pauli-Z gate acts on a single qubit. It equates to a rotation around the Z-axis of the Bloch sphere by ? radians. It leaves the basis state |0? and maps |1? to ?|1?

The Pauli Z matrix is defined as: \(Z = \begin{bmatrix}1 \ 0 \\ 0 \ -1 \end{bmatrix}\)

\(Z * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\)

Other gates are described in this link: https://en.wikipedia.org/wiki/Quantum_gate

State measurement

State measurement can be done using polarizing filters. Filters transmit or block particles based on angle of polarization.

IBM Q

IBM Q is a cloud quantum computing platform.

Below a simple experiment where we have two qubits. No transformation is applied on first qubit. A Pauli X transformation is applied on second qubit. As result there is one possible state |10? with probability equals 1.

Data representation

Given a vector \(x = (x_1, x_2, . , x_n)\). The quantum system topology needed to store the vector x is \(log_2(n)\) qubits.

For example, the quantum system representation of the following vector requires only 3 qubits.

(0, 0.2, 0.2, 0, 0.1, 0.2, 0.1, 0.3) ? 0 |000? + 0.2 |001? + 0.2 |010? + 0 |011? + 0.1 |100? + 0.2 |101? + 0.1 |110? + 0.3 |111?

by Sadek

Neural Network

A neural network is a non-linear classifier (separator is not a linear function). It can also be used for regression.

A Shallow neural network is a one hidden layer neural network.

A Vanilla neural network is a regular neural network having layers that do not form cycles.

TensorFlow Playground is an interactive web interface for learning neural networks: http://playground.tensorflow.org.

Computational Graph

Above the computational graph for the function \(f(x) = (x-1)^2\).

Forward propagation

To minimize the function f, we assign a random value to x (e.g. x = 2), then we evaluate y, z, and f (forward propagation).

Backward propagation

Then we compute the partial derivative of f with respect to x step by step (Backward propagation).

\(\frac{\partial f}{\partial x} = \frac{\partial f}{\partial y}*\frac{\partial y}{\partial x} + \frac{\partial f}{\partial z}*\frac{\partial z}{\partial x} = 2 \\ \frac{\partial f}{\partial y} = z = 1 \\ \frac{\partial f}{\partial z} = y = 1 \\ \frac{\partial y}{\partial x} = \frac{\partial z}{\partial x} = 1\)

Then we update \(x:= x – ?.\frac{\partial f}{\partial x}\).

We repeat the operation until convergence.

Activation functions

Activation functions introduce nonlinearity into models. The most used activation functions are:

Sigmoid

\(f(x) = \frac{1}{1+exp(-x)}\)

Sigmoid has a positive and non-zero centred output (sigmoid(0) ? 0.5).

When all activation units are positive, then weight update will be in the same direction (all positive or all negative updates) and that will cause a zigzag path during optimization.

\(z=?w_i.a_i+b \\ \frac{dL}{dw_i}=\frac{dL}{dz}.\frac{dz}{dw_i}=\frac{dL}{dz}.ai\)

If all ai>0, then the gradient will have the same sign as \(\frac{dL}{dz}\) (all positive or all negative).

TanH

\(f(x) = \frac{2}{1+exp(-2x)} -1\)

When x is large, the derivative of the sigmoid or Tanh function is around zero (vanishing gradient/saturation).

ReLU (Rectified Linear Unit)

f(x) = max(0, x)

Leaky ReLU

f(x) = max(0.01x, x)

Leaky Relu was introduced to fix the Dying Relu problem.

\(z=?w_i.a_i+b \\ f=Relu(z) \\ \frac{dL}{dw_i}=\frac{dL}{df}.\frac{df}{dz}.\frac{dz}{dw_i}\)

When z becomes negative, then the derivative of f becomes equal to zero, and the weights stop being updated.

PRelu (Parametric Rectifier)

f(x) = max(?.x, x)

ELU (Exponential Linear Unit)

f(x) = {x if x>0 otherwise ?.(exp(x)-1)}

Other activation functions: Maxout

Cost function

\(J(?) = \frac{1}{m} \sum_{i=1}^{m} loss(y^{(i)}, f(x^{(i)}; ?))\)

We need to find ? that minimizes the cost function: \(\underset{?}{argmin}\ J(?)\)

Neural Network Regression

Neural Network regression has no activation function at the output layer.

L1 Loss function

\(loss(y,?) = |y – ?|\)

L2 Loss function

\(loss(y,?) = (y – ?)^2\)

Hinge loss function

Hinge loss function is recommended when there are some outliers in the data.

\(loss(y,?) = max(0, |y-?| – m)\)

Two-Class Neural Network

Binary Cross Entropy Loss function

\(loss(y,?) = – y.log(?) – (1-y).log(1 – ?)\)

Multi-Class Neural Network – One-Task

Using Softmax, the output ? is modeled as a probability distribution, therefore we can assign only one label to each example.

Cross Entropy Loss function

\(loss(Y,\widehat{Y}) = -\sum_{j=1}^c Y_{j}.log(\widehat{Y}_{j})\)

Hinge Loss (SVM) function

\(y = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix},\ ? = \begin{bmatrix} 2 \\ -5 \\ 3 \end{bmatrix} \\ loss(y,?) = \sum_{c?1} max(0, ?_c – ?_1 + m)\)

For m = 1, the sum will be equal to 2.

Multi-Class Neural Network – Multi-Task

In this version, we assign multiple labels to each example.

Loss function

\(loss(Y,\widehat{Y}) = \sum_{j=1}^c – Y_j.log(\widehat{Y}_j) – (1-Y_j).log(1 – \widehat{Y}_j)\)

Regularization

Regularization is a very important technique to prevent overfitting.

Dropout

For each training example, ignore randomly p activation nodes of each hidden layer. p is called dropout rate (p?[0,1]). When testing, scale activations by the dropout rate p.

Inverted Dropout

With inverted dropout, scaling is applied at the training time, but inversely. First, dropout all activations by dropout factor p, and second, scale them by inverse dropout factor 1/p. Nothing needs to be applied at test time.

Data Augmentation

As a regularization technique, we can apply random transformations on input images when training a model.

Early stopping

Stop when error rates decreases on training data while it increases on dev (cross-validation) data.

L1 regularization

\(J(?) = \frac{1}{m} \sum_{i=1}^{m} loss(y^{(i)}, f(x^{(i)}; ?)) \color{blue} { + ? .\sum_{j} |?_j|} \)

? is called regularization parameter

L2 regularization

\(J(?) = \frac{1}{m} \sum_{i=1}^{m} loss(y^{(i)}, f(x^{(i)}; ?)) \color{blue} { + ? .\sum_{j} ?_j^2} \)

Lp regularization

\(J(?) = \frac{1}{m} \sum_{i=1}^{m} loss(y^{(i)}, f(x^{(i)}; ?)) \color{blue} { + ? .\sum_{j} ?_j^p} \)

For example, if the cost function \(J(?)=(?_1 – 1)^2 + (?_2 – 1)^2\), then the \(L_2\) regularized cost function is \(J(?)=(?_1 – 1)^2 + (?_2 – 1)^2 + ? (?_1^2 + ?_2^2)\)

If ? is large, then the point that minimizes the regularized J(?) will be around (0,0) –> Underfitting.

If ? ~ 0, then the point that minimizes the regularized J(?) will be around (1,1) –> Overfitting.

Elastic net

Combination of L1 and L2 regularizations.

Normalization

Gradient descent converges quickly when data is normalized Xi ? [-1,1]. If features have different scales, then the update of parameters will not be in the same scale (zig-zag).

For example, if the activation function g is the sigmoid function, then when W.x+b is large g(W.x+b) is around 1, but the derivative of the sigmoid function is around zero. For this reason the gradient converges slowly when the W.x+b is large.

Below some normalization functions.

ZScore

\(X:= \frac{X – ?}{?}\)

MinMax

\(X:= \frac{X – min}{max-min}\)

Logistic

\(X:= \frac{1}{1+exp(-X)}\)

LogNormal

\(X:= \frac{1}{?\sqrt{2?}} \int_{0}^{X} \frac{exp(\frac{-(ln(t) – ?)^2}{2?^2})}{t} dt\)

Tanh

\(X:= tanh(X)\)

Weight Initialization

Weight initialization is important because if weights are too big then activations explode. If weights are too small then gradients will be around zero (no learning).

When we normalize input data, we make the mean of the input features equals to zero, and the variance equals to one. To keep the activation units normalized too, we can initialize the weights \( W^{(1)}\) so \(Var(g(W_{j}^{(1)}.x+b_{j}^{(1)}))\) is equals to one.

If we suppose that g is Relu and \(W_{i,j}, b_j, x_i\) are independent, then:

\(Var(g(W_{j}^{(1)}.x+b_{j}^{(1)})) = Var(\sum_{i} W_{i,j}^{(1)}.x_i+b_{j}^{(1)}) =\sum_{i} Var(W_{i,j}^{(1)}.x_i) + 0 \\ = \sum_{i} E(x_i)^2.Var(W_{i,j}^{(1)}) + E(W_{i,j}^{(1)})^2.Var(x_i) + Var(W_{i,j}^{(1)}).Var(x_i) \\ = \sum_{i} E(x_i)^2.Var(W_{i,j}^{(1)}) + E(W_{i,j}^{(1)})^2.Var(x_i) + Var(W_{i,j}^{(1)}).Var(x_i) \\ = \sum_{i} 0 + 0 + Var(W_{i,j}^{(1)}).Var(x_i) = n.Var(W_{i,j}^{(1)}).Var(x_i) \)

Xavier initialization

If we define \(W_{i,j}^{(1)} ? N(0,\frac{1}{\sqrt{n}})\), then the initial variance of activation units will be one (n is number of input units).

We can apply this rule on all weights of the neural network.

Batch Normalization

Batch normalization is a technique to provide any layer in a Neural Network with normalized inputs. Batch Normalization has a regularizing effect.

After training, ? will converge to the standard deviation of the mini-batches and ? will converge to the mean. The ?, ? parameters give more flexibility when shifting or scaling is needed.

Hyperparameters

Neural network hyperparameters are:

  • Learning rate (?) (e.g. 0.1, 0.01, 0.001,…)
  • Number of hidden units
  • Number of layers
  • Mini-bach size
  • Momentum rate (e.g. 0.9)
  • Adam optimization parameters (e.g. ?1=0.9, ?2=0.999, ?=0.00000001)
  • Learning rate decay

Local Minimum

The probability that gradient descent gets stuck in a local minimum in a high dimensional space is extremely low. We could have a saddle point, but its rare to have a local minimum.

Transfer Learning

Transfer Learning consists in the use of parameters of a trained model when training new hidden layers of an extended version of that model.

by Sadek

Machine Learning Algorithms – Summary

Characteristics of Machine Learning Algorithms

Discriminative / Generative algorithms

Many machine learning algorithms are based on probabilistic models. Discriminative algorithms learn the conditional probability distribution of y given x p(y|x). Generative algorithms learn the joint probability distribution p(y,x) = p(y|x) * p(x), and therefore take in consideration the distribution of x.

Parametric & Non-Parametric algorithms

Neural Network, SVM,… are non-parametric algorithms because they have no fixed parameter vector; depending on the richness of the data we can choose the size of the parameter vector that we need (ex. we can add hidden units, change SVM kernels,…)

Capacity

The capacity is controlled by parameters called Hyperparameters (ex. degree p of a polynomial predictor, kernel choice in SVM, number of layers in a neural network).

Summary of Machine Learning Algorithms

The table below describes briefly each machine learning algorithm.

Algorithm

Description

Characteristics

Linear regression

To use when Y is normally-distributed

Discriminative

Parametric

Logistic regression

To use when Y is Bernoulli-distributed

Discriminative

Parametric

Multinomial logistic regression (softmax regression)

To use when Y is multinomially-distributed

There are two versions of the algorithm, one based on maximum likelihood maximization, and one based on cross-entropy minimization.

Discriminative

Parametric

Gaussian Discriminant Analysis

Supervised classification algorithm

To use when Y is Bernoulli distributed and the conditional distribution of X given Y is multivariate Gaussian

Generative

Parametric

Naive Bayes Algorithm

Supervised classification algorithm

To use when Y is Bernoulli, and the conditional distribution of X given Y is Bernoulli and X features are conditionally independent

Generative

Parametric

EM

Unsupervised soft-clustering algorithm

Generative

Parametric

Principal Component Analysis

Reduce the dimensionality of X.

Calculate eigenvectors for \(XX^T\). Use eigenvectors with higher eigenvalues to transform data \(x^{(i)} := (u_1^T x^{(i)}, u_2^T x^{(i)},…, , u_k^T x^{(i)})\)

Factor Analysis

Reduce the dimensionality of X

To use when X is Gaussian.

Transform X to Z matrix with lower dimensionality (x ? ?+?z).

Neural Network

Non-linear classifier

Discriminative

Non-Parametric

K-Nearest Neighbor Regression

Predict y as the average of values y1,y2,,yk of k nearest neighbors of x

Discriminative

Non-Parametric

K-Nearest Neighbor Classifier

Predict y as the most common class among the k nearest neighbors of x

Discriminative

Non-Parametric

Support Vector Machine

Find a separator that maximizes the margin between two classes

Discriminative

Non-Parametric

K-means

Unsupervised hard-clustering algorithm

Discriminative

Non-Parametric
by Sadek

What’s next!

Without any doubt Machine Learning / Artificial Intelligence will drastically change the world during the next decade. Deep Learning algorithms are reaching unprecedentedly high level of accuracy, but they are slow to train. For this reason Big companies are working on a design of new chips optimized to run Deep Learning algorithms.

Machine Learning Research Scientists

Below the list of some known Machine Learning research scientists:

Geoffrey Hinton

Former University of Toronto professor.

The godfather of neural network research.

Andrew Ng

Adjunct professor at Stanford University.

Founder of Google Brain project.

Yann LeCun

Director of AI Research at Facebook.

Founding father of convolutional neural network.

Yoshua Bengio

Full professor at Universit de Montral.

One of the founding fathers of deep learning.

Machine Learning Platforms

Microsoft Azure ML: https://studio.azureml.net/

Google ML: https://cloud.google.com/ml/

Amazon ML: http://aws.amazon.com/machine-learning/

Machine Learning Frameworks

Caffe2(Facebook), PyTorch(Facebook), Tensorflow(Google), Paddle(Baidu), CNTK(Microsoft), MXNet(Amazon).

High-Performance Hardware for Machine Learning

GPGPU Architecture

General-purpose computing on graphics processing units is the use of a graphics processing unit (GPU) to perform computations in applications traditionally handled by the central processing unit (CPU). There are GPU programming frameworks that allow the use of GPUs for general purpose tasks. The widely used frameworks are Cuda and OpenCL. Cuda is supported only on NVIDIA GPUs. OpenCL is open standard, it’s supported on most recent Intel and AMD GPUs.

FPGA Architecture

FPFAs are hardware implementations of algorithms, and hardware is always faster than software. A use of a multiple-FPGA parallel computing architecture can dramatically improve computing performance.

Tensor Processing Unit

TPUs are application-specific integrated circuits developed specifically for machine learning. They are designed explicitly for a higher volume of reduced precision computation (as little as 8-bit precision).

https://en.wikipedia.org/wiki/Tensor_processing_unit.

by Sadek

Statistics

Basic Statistics

Basic statistics for a discrete variable X:

Mean(μ) = Expect Value E[X]

=\(\frac{1}{n} \sum_{i=1}^{n} x_{i} \)

Median

If n is odd then \(x_{\frac{n+1}{2}}\) else \(\frac{x_{\frac{n}{2}} + x_{\frac{n+2}{2}}}{2}\)

Variance (\(\sigma^{2}=E_{x \sim p(x)}[(X-E[X])^2]\))

(n-1 is called degree of freedom)

=\(\frac{1}{n-1}\sum_{i=1}^{n} (x_{i} -\mu)^{2}\)

Standard deviation (\(\sigma\))

=\(\sqrt{\sigma^{2}}\)

Mode

is the value x at which its probability mass function takes its maximum value. For example the mode of {1,1,1,2,2,3,4} is 1 because it appears 3 times

Covariance(X,Y)

 \(= E[(X-E[X])(Y-E[Y])]\) \(= E[XY] -E[X]E[Y]\) \(= \frac{1}{n-1} \sum_{i=1}^{n} (X_i – μ_X)(Y_i – μ_Y)\)

Correlation(X,Y)

=\(\frac{Covariance(X,Y)}{\sqrt{Var(X).Var(Y)}}\)

Standard error

 \(= \frac{σ}{\sqrt{n}}\)

Basic statistics for a continuous variable X:

Mean(μ) = Expect Value E[X]

=\(\int_{all\, x} p(x)\,x\,dx\)

Median

m such as p(x<=m) = .5

Variance (\(\sigma^{2}=E_{x \sim p(x)}[(X-E[X])^2]\))

=\(\int_{all\, x} p(x)\,(x -\mu)^{2}\,dx\)

Standard deviation (\(\sigma\))

=\(\sqrt{\sigma^{2}}\)

Mode

is the value x at which its probability density function has its maximum value

Examples:

For a set {-1, -1, 1, 1} => Mean = 0, Variance = 1.33, Standard deviation = 1.15

If \(x \in [0, +\infty]\) and p(x) = exp(-x) => Mean = 1, Variance = 1, Standard deviation = 1

Expected value

Expectations are linear. E[X+Y] = E[X] + E[Y]

Probability Distributions

A random variable is a set of outcomes from a random experiment.

A probability distribution is a function that returns the probability of occurrence of an outcome. For discrete random variables, this function is called “Probability Mass Function”. For continuous variables, this function is called “Probability Density Function”.

A joint probability distribution is a function that returns the probability of joint occurrence of outcomes from two or more random variables. If random variables are independent then the joint probability distribution is equal to the product of the probability distribution of each random variable.

A conditional probability distribution is the probability distribution of a random variable given another random variables.

Example:

X

P(X)

A

0.2

B

0.8

P(X) is the probability distribution of X.

Y

P(Y)

C

0.1

D

0.9

P(Y) is the probability distribution of Y.

X

Y

P(X,Y)

A

C

0.1

A

D

0.1

B

D

0.8

P(X,Y) is the joint probability distribution of X and Y.

X

P(X|Y=D) = P(X,Y)/P(Y=D)

A

0.1/0.9

B

0.8/0.9

P(X|Y=D) is the conditional probability distribution of X given Y = D.

Marginal probability

Sometimes we know the probability distribution over a set of variables and we want to know the probability distribution over just a subset of them. The probability distribution over the subset is known as the marginal probability distribution.

For example, suppose we have discrete random variables x and y, and we know P(x, y). We can find P(x) with the sum rule: \(P(x) = \sum_y P(x,y)\)

Below the statistical properties of some distributions.

Binomial distribution

Nb of output values = 2 (like coins)

n = number of trials

p = probability of success

P(X) = \(C_n^X * p^{X} * (1-p)^{n-X}\)

Expected value = n.p

Variance = n.p.(1-p)

Example:

If we flip a fair coin (p=0.5) three time (n=3), what’s the probability of getting two heads and one tail?

P(X=2) = P(2H and 1T) = P(HHT + HTH + THH) = P(HHT) + P(HTH) + P(THH) = p.p(1-p) + p.(1-p).p + (1-p).p.p = \(C_3^2.p^2.(1-p)\)

Bernoulli distribution

Bernoulli distribution is a special case of the binomial distribution with n=1.

Nb of output values = 2 (like coins)

n = 1 (number of trials)

p = probability of success

X \(\in\) {0,1}

P(X) = \(p^{X} * (1-p)^{1-X}\)

Expected value = p

Variance = p.(1-p)

Example:

If we flip a fair coin (p=0.5) one time (n=1), what’s the probability of getting 0 head?

P(X=0) = P(0H) = P(1T) = 1-p = \(p^0.(1-p)^1\)

Multinomial distribution

It’s a generalization of Binomial distribution. In a Multinomial distribution we can have more than two outcomes. For each outcome, we can assign a probability of success.

Normal (Gaussian) distribution

P(x) = \(\frac{1}{\sigma \sqrt{2\pi}} exp(-\frac{1}{2} (\frac{x-\mu}{\sigma})^{2})\)

σ and μ are sufficient statistics (sufficient to describe the whole curve)

Expected value = \(\int_{-\infty}^{+\infty} p(x) x \, dx\)

Variance = \(\int_{-\infty}^{+\infty} (x – \mu)^2 p(x) \, dx\)

Standard Normal distribution (Z-Distribution)

It’s a normal distribution with mean = 0 and standard deviation = 1.

P(z) = \(\frac{1}{\sqrt{2\pi}} exp(-\frac{1}{2} z^2)\)

Cumulative distribution function:

\(P(x \leq z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} exp(-\frac{1}{2} x^2) \, dx\)

Exponential Family distribution

\(P(x;\theta) = h(x)\exp \left(\eta (θ)\cdot T(x)-A(θ)\right) \), where T(x), h(x), η(θ), and A(θ) are known functions.

θ = vector of parameters.

T(x) = vector of “sufficient statistics”.

A(θ) = cumulant generating function.

The Binomial distribution is an Exponential Family distribution

\(P(x)=C_n^x\ p^{x}(1-p)^{n-x},\quad x\in \{0,1,2,\ldots ,n\}\)

This can equivalently be written as:

\(P(x)=C_n^x\ exp (log(\frac{p}{1-p}).x – (-n.log(1-p)))\)

The Normal distribution is an Exponential Family distribution

Consider a random variable distributed normally with mean μ and variance \(σ^2\). The probability density function could be written as: \(P(x;θ) = h(x)\exp(η(θ).T(x)-A(θ)) \)

With:

\(h(x)={\frac{1}{\sqrt {2\pi \sigma ^{2}}}}exp^{-{\frac {x^{2}}{2\sigma ^{2}}}}\) \(T(x)={\frac {x}{\sigma }}\) \(A(\mu)={\frac {\mu ^{2}}{2\sigma ^{2}}}\) \(\eta(\mu)={\frac {\mu }{\sigma }}\)

Poisson distribution

The Poisson distribution is popular for modelling the number of times an event occurs in an interval of time or space (eg. number of arrests, number of fish in a trap…).

In a Poisson distribution, values are discrete and can’t be negative.

The probability mass function is defined as: \(P(x=k)=\frac{λ^k.e^{-λ}}{k!}\), k is the number of occurrences. λ is the expected number of occurrences.

Exponential distribution

The exponential distribution has a probability distribution with a sharp point at x = 0.

\(P(x; λ) = λ.1_{x≥0}.exp (−λx)\)

Laplace distribution

Laplace distribution has a sharp peak of probability mass at an arbitrary point μ. The probability mass function is defined as \(Laplace(x;μ,γ) = \frac{1}{2γ} exp(-\frac{|x-μ|}{γ})\)

Laplace distribution is a distribution that is symmetrical and more “peaky” than a normal distribution. The dispersion of the data around the mean is higher than that of a normal distribution. Laplace distribution is also sometimes called the double exponential distribution.

Dirac distribution

The probability mass function is defined as \(P(x;μ) = δ(x).(x-μ)\) such as δ(x) = 0 when x ≠ μ and \(\int_{-∞}^{∞} δ(x).(x-μ) dx= 1\).

Empirical Distribution

Other known Exponential Family distributions

Dirichlet.

Laplace Smoothing

Given a set S={a1, a1, a1, a2}.

Laplace smoothed estimate for P(x) with domain of x in {a1, a2, a3}:

\(P(x=a1)=\frac{3 + 1}{4 + 3}\) \(P(x=a2)=\frac{1 + 1}{4 + 3}\) \(P(x=a3)=\frac{0 + 1}{4 + 3}\)

Maximum Likelihood Estimation

Given three independent data points \(x_1=1, x_2=0.5, x_3=1,5\), what the mean μ of a normal distribution that these three points are more likely to come from (we suppose the variance=1).

If μ = 4, then the probabilities \(P(X=x_1), P(X=x_2), P(X=x_3)\) will be low, and \(P(x_1,x_2,x_3) = P(X=x_1)*P(X=x_2)*P(X=x_3)\) will be also low.

If μ = 1, then the probabilities \(P(X=x_1), P(X=x_2), P(X=x_3)\) will be high, and \(P(x_1,x_2,x_3) = P(X=x_1)*P(X=x_2)*P(X=x_3)\) will be also high. Which means that the three points are more likely to come from a normal distribution with mean μ = 1.

The likelihood function is defined as: \(P(x_1,x_2,x_3; μ)\)

Central Limit Theorem

The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement , then the distribution of sample means will be approximately normally distributed.

Bayesian Network

X1, X2 are random variables.

P(X1,X2) = P(X2,X1) = P(X2|X1) * P(X1) = P(X1|X2) * P(X2)

P(X1) is called prior probability.

P(X1|X2) is called posterior probability.

Example:

A mixed school having 60% boys and 40% girls as students. The girls wear trousers or skirts in equal numbers; the boys all wear trousers. An observer sees from a distance a student wearing a trouser. What is the probability this student is a girl?

The prior probability P(Girl): 0.4

The posterior probability P(Girl|Trouser): \(\frac{P(Trouser|Girl)*P(Girl)}{P(Trouser|Girl) * P(Girl) + P(Trouser|Boy) * P(Boy)} = 0.25\)

Parameters estimation – Bayesian Approach Vs Frequentist Approach

There are two approaches that can be used to estimate the parameters of a model.

Frequentist approach

Bayesian approach
\(arg\ \underset{θ}{max} \prod_{i=1}^m P(y^{(i)}|x^{(i)};θ)\) \(arg\ \underset{θ}{max} P(θ|\{(x^{(i)}, y^{(i)})\}_{i=1}^m)\) \(=arg\ \underset{θ}{max} \frac{P(\{(x^{(i)}, y^{(i)})\}_{i=1}^m|θ) * P(θ)}{P(\{(x^{(i)}, y^{(i)})\}_{i=1}^m)}\) \(=arg\ \underset{θ}{max} P(\{(x^{(i)}, y^{(i)})\}_{i=1}^m|θ) * P(θ)\)

If \(\{(x^{(i)}, y^{(i)})\}\) are independent, then:

\(=arg\ \underset{θ}{max} \prod_{i=1}^m P((y^{(i)},x^{(i)})|θ) * P(θ)\)

To calculate P(θ) (called the prior), we assume that θ is Gaussian with mean 0 and variance \(\sigma^2\).

\(=arg\ \underset{θ}{max} log(\prod_{i=1}^m P((y^{(i)},x^{(i)})|θ) * P(θ))\) \(=arg\ \underset{θ}{max} log(\prod_{i=1}^m P((y^{(i)},x^{(i)})|θ)) + log(P(θ))\)

after some few derivations, we will find the the expression is equivalent to the L2 regularized linear cost function.

\(=arg\ \underset{θ}{min} \frac{1}{2} \sum_{i=1}^{n} (y^{(i)}-h_{θ}(x^{(i)}))^{2} + λ θ^Tθ\)

Because of the prior, Bayesian algorithms are less susceptible to overfitting.

Cumulative distribution function (CDF)

Given a random continuous variable S with density function p(s). The Cumulative distribution function \(F(s) = p(S<=s) = \int_{-∞}^{s} p(s) ds\)

F'(s) = p(s)

by Sadek

Math Review

Linear Algebra

A matrix is a 2-D array of numbers.

A tensor is a n-D array of numbers.

Matrices are associative but not commutative.

Not all square matrices have inverse. A matrix that is not invertible is called Singular or Degenerative.

A matrix is “singular” if any of the following are true:

-Any row or column contains all zeros.

-Any two rows or columns are identical.

-Any row or column is a linear combination of other rows or columns.

A square matrix A is singular, if and only if the determinant(A) = 0

Inner product of two vectors \(\overrightarrow{u}\) and \(\overrightarrow{v}\):

\(\overrightarrow{u} * \overrightarrow{v} = p * ||\overrightarrow{u}|| = p * \sqrt{\sum_{i=1}^{n}u_{i}^{2}} = u^{T} * v = \sum_{i=1}^{n}u_{i} * v_{i}\)

p is the projection of \(\overrightarrow{v}\) on \(\overrightarrow{u}\) and \(||\overrightarrow{u}||\) is the Euclidean norm of \(\overrightarrow{u}\).

\(A = \begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix}\)

Determinant(A) = |A| = a(ei-hf) – b(di-gf) + c(dh – ge)

If \(f: R^{n*m} \mapsto R\)

\(\frac{\partial}{\partial A} f(A) = \begin{bmatrix} \frac{\partial}{\partial a_{11}}f(A) & … & \frac{\partial}{\partial a_{1m}} f(A)\\ … & … & …\\ \frac{\partial}{\partial a_{n1}}f(A) & … & \frac{\partial}{\partial a_{nm}}A\\ \end{bmatrix}\)

Example:

\( f(A) = a_{11} + … + a_{nm} \)

\(\frac{\partial}{\partial A} f(A) = \begin{bmatrix} 1 & … & 1\\ … & … & …\\ 1 & … & 1 \\ \end{bmatrix}\)

If A is a squared matrix:

trace(A) = \(\sum_{i=1}^n A_{ii}\)

trace(AB) = trace(BA)

trace(ABC) = trace(CAB) = trace(BCA)

trace(B) = trace(\(B^T\))

trace(a) = a

\(\frac{\partial}{\partial A} trace(AB) = B^T\) \(\frac{\partial}{\partial A} trace(ABA^TC) = CAB + C^TAB^T\)

Eigenvector

Given a matrix A, if a vector μ satisfies the equation A*μ = λ*μ then μ is called an eigenvector for the matrix A, and λ is called the eigenvalue for the matrix A. The principal eigenvector for the matrix A is the eigenvalue with the largest eigenvalue.

Example:

The normalized eigenvectors for \(\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix}\) are \(\begin{bmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\) and \(\begin{bmatrix}-\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\), the eigenvalues are 1 and -1.

Eigendecomposition

Given a squared matrix A∈\(R^{n*n}\), ∃ Q∈\(R^{n*n}\), Λ∈\(R^{n*n}\) and Λ diagonal, such as \(A=QΛQ^T\).

Q’s columns are the eigenvectors of \(A\)

Λ is the diagonal matrix whose diagonal elements are the eigenvalues

Example:

The eigendecomposition of \(\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix}\) is Q=\(\begin{bmatrix}\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{bmatrix}\), Λ=\(\begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{bmatrix}\)

Eigenvectors are vect

Single Value Decomposition

Given a matrix A∈\(R^{n*m}\), ∃ U∈\(R^{n*m}\), D∈\(R^{m*m}\) and D diagonal, V∈\(R^{m*m}\) such as \(A=UDV^T\).

U’s columns are the eigenvectors of \(AA^T\)

V’s columns are the eigenvectors of \(A^TA\)

Example:

The SVD decomposition of \(\begin{bmatrix} 0 & 1 \\1 & 0 \end{bmatrix}\) is U=\(\begin{bmatrix}0 & -1 \\ -1 & 0\end{bmatrix}\), D=\(\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\), V=\(\begin{bmatrix}-1 & 0 \\ 0 & -1\end{bmatrix}\).

More details about SVD can be found here: http://www.youtube.com/watch?v=9YtmGy-wfE4

The Moore-Penrose Pseudoinverse

The Moore-Penrose pseudoinverse is a matrix that can act as a partial replacement for the matrix inverse in cases where it does not exist (e.g. non-square matrices).

The pseudoinverse matrix is defined as: \(pinv(A) = \lim_{α \rightarrow 0} (A^TA + αI)^{-1} A^T\)

Analysis

0! = 1

exp(1) = 2.718

exp(0) = 1

ln(1) = 0

\(ln(x) = log_e(x) \\ log_b (b^a) = a\)

exp(a + b) = exp(a) * exp(b)

ln(a * b) = ln(a) + ln(b)

\(cos(x)^2 + sin(x)^2 = 1\)

Euler’s formula

exp(iθ) = cos(θ) + i sin(θ)

Complex numbers

Rectangular form

z = a + ib (real part + imaginary part and i an imaginary unit satisfying \(i^2 = −1\)).

Polar form

z = r (cos(θ) + i sin(θ))

Exponential form

z = r.exp(iθ)

Multivariate equations

The solution set of a system of linear equations with 3 variables is the intersection of hyperplanes defined by each linear equation.

Derivatives

\(\frac{\partial f(x)}{\partial x} = \lim_{h \rightarrow 0} \frac{f(x+h) – f(x)}{h}\)

Function

Derivative

x^n

n * x^(n-1)

exp(x)

exp(x)

f o g (x)

g’(x) * f’ o g(x)

ln(x)

1/x

sin(x)

cos(x)

cos(x)

-sin(x)

Integration by parts

\(\int_{a}^{b} (f(x) g(x))’ dx = \int_{a}^{b} f'(x) g(x) dx+ \int_{a}^{b} f(x) g'(x) dx\)

Binomial theorem

\((x + y)^n = \sum_{k=0}^{n} C_n^k x^k y^{n-k}\)

Chain rule

Z = f(x(u,v), y(u,v))

\(\frac{\partial Z}{\partial u} = \frac{\partial Z}{\partial x} * \frac{\partial x}{\partial u} + \frac{\partial Z}{\partial y} * \frac{\partial y}{\partial u}\)

Entropy

Entropy measures the uncertainty associated with a random variable.

\(H(X) = -\sum_{i=1}^n p(x^{(i)}) log(p(x^{(i)}))\)

Example:

Entropy({1,1,1,1}) = 0

Entropy({0,1,0,1}) = -½ (4*log(½))

Hessian

\(H = \begin{bmatrix}\frac{\partial^2 f(θ)}{\partial θ_1\partial θ_1} & \frac{\partial^2 f(θ)}{\partial θ_1 \partial θ_2} \\ \frac{\partial^2 f(θ)}{\partial θ_2\partial θ_1} & \frac{\partial^2 f(θ)}{\partial θ_2\partial θ_2} \end{bmatrix}\)

Example:

\(f(θ) = θ_1^2 + θ_2^2 \\ H(f) = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}\)

A function f(θ) is convex if its Hessian matrix is positive semidefinite (\(x^T.H(θ).x >= 0\), for every \(x∈R^2\)).

\(x^T.H(θ).x = \begin{bmatrix} x_1 & x_2 \end{bmatrix} . \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} . \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = 2 x_1^2 + 2 x_2^2 >= 0\)

Method of Lagrange Multipliers

To maximize/minimize f(x) with the constraints \(h_r(x) = 0\) for r in {1,..,l},

We need to define the Lagrangian: \(L(x, α) = f(x) – \sum_{r=1}^l α_r h_r(x)\) and find x, α by solving the following equations:

\(\frac{\partial L}{\partial x} = 0\)

\(\frac{\partial L}{\partial α_r} = 0\) for all r

\(h_r(x) = 0\) for all r

Calculate the Hessian matrix (f”(x)) to know if the solution is a minimum or maximum.

Method of Lagrange Multipliers with inequality constraints

To minimize f(x) with the constraints \(g_i(x) \geq 0\) for i in {1,..,k} and \(h_r(x) = 0\) for r in {1,..,l},

We need to define the Lagrangian: \(L(x, α, β) = f(w) – \sum_{i=1}^k α_i g_i(x) – \sum_{r=1}^l β_r h_r(x)\) and find x, α, β by solving the following equations:

\(\frac{\partial L}{\partial x} = 0\)

\(\frac{\partial L}{\partial α_i} = 0\) for all i

\(\frac{\partial L}{\partial β_r} = 0\) for all r

\(h_r(x) = 0\) for all r

\(g_i(x) \geq 0\) for all i

\(α_i * g_i(x) = 0\) for all i (Karush–Kuhn–Tucker conditions)

\(α_i >= 0\) for all i (KTT conditions)

Lagrange strong duality – hard to understand 🙁

Lagrange dual function \(d(α, β) = \underset{x}{min} L(x, α, β)\), and x satisfies equality and inequality constraints.

We define \(d^* = \underset{α \geq 0, β}{max}\ d(α, β)\)

We define \(p^* = \underset{w}{min}\ f(x) \) (x satisfies equality and inequality constraints)

Under certain conditions (Slater conditions: f convex,…), \(p^* = d^*\)

Jensen’s inequality

If f a convex function, and X a random variable, then f(E[X]) <= E[f(X)].

If f a concave function, and X a random variable, then f(E[X]) >= E[f(X)].

If f is strictly convex (f”(x) > 0), then f(E[X]) = E[f(X)] holds true only if X = E[X] (X is a constant).

Probability

Below the main probability theorems.

Law of total probability

If A is an arbitrary event, and B are mutually exclusive events such as \(\sum_{i=1}^{n} P(B_{i}) = 1\), then:

\(P(A) = \sum_{i=1}^{n} P(A|B_{i}) P(B_{i}) = \sum_{i=1}^{n} P(A,B_{i})\)

Example:

Suppose that 15% of the population of your country was exposed to a dangerous chemical Z. If exposure to Z quadruples the risk of lung cancer from .0001 to .0004. What’s the probability that you will get lung cancer.

P(cancer) = .15 * .0004 + .85 * .0001 = .000145

Bayes’ rule

P(A|B) = P(B|A) * P(A) / P(B)

Where A and B are events.

Example:

Suppose that 15% of the population of your country was exposed to a dangerous chemical Z. If exposure to Z quadruples the risk of lung cancer from .0001 to .0004. If you have lung cancer, what’s the probability that you were exposed to Z?

P(Z|Cancer) = P(Cancer|Z) * P(Z) / P(Cancer)

We can calculate the P(Cancer) using the law of total probability: P(Cancer) = P(Cancer|Z) * P(Z) + P(Cancer|~Z) * P(~Z)

P(Z|Cancer) = .0004 * 0.15 / (.0004 * 0.15 + .0001 * .85) = 0.41

Chain rule

\(P(A_1,A_2,…,A_n) = P(A_1) P(A_2|A_1) ….P(A_n|A_{n-1},…,A_1)\)

P(Y,X1,X2,X3,X4) = P(Y,X4,X3,X2,X1)

= P(Y|X4,X3,X2,X1) * P(X4|X3,X2,X1) * P(X3|X2,X1) * P(X2|X1) * P(X1)

= P(Y|X4,X3) * P(X4) * P(X3|X2,X1) * P(X2) * P(X1)

The Union Bound

\(P(A_1 \cup A_2 … \cup A_n) \leq P(A_1) + P(A_2) + … + P(A_n) \)

Nb of permutations with replacement

Nb of permutations with replacement = \({n^r}\), r the number of events, n the number of elements.

Probability = \(\frac{1}{n^r}\)

Example:

Probability of getting 3 six when rolling a dice = 1/6 * 1/6 * 1/6

Probability of getting 3 heads when flipping a coin = 1/2 * 1/2 * 1/2

Nb of permutations without replacement and with ordering

Nb of permutations without replacement = \(\frac{n!}{(n-r)!}\), r the number of events, n the number of elements.

Probability = \(\frac{(n-r)!}{n!}\)

Example:

Probability of getting 1 red ball and then 1 green ball from an urn that contains 4 balls (1 red, 1 green, 1 black and 1 blue) = 1/4 * 1/3

Nb of combinations without replacement and without ordering

Nb of combinations \(\frac{n!}{(n-r)! \, r!}\), r the number of events, n the number of elements.

Probability = \(\frac{(n-r)! \, r!}{n!}\)

Example:

Probability of getting 1 red ball and 1 green ball from an urn that contains 4 balls (1 red, 1 green, 1 black and 1 blue) = 1/4 * 1/3 + 1/4 * ⅓

by Sadek

SSAS Tabular

SSAS Architecture

SSAS Server Modes

There are three SSAS Server Modes: Multidimensional, Tabular and Sharepoint.

SSAS Tabular Architecture

Tabular Model

Its recommended to use views instead of tables when adding tabular model tables.

View names, column names and tabular table/column names should be user friendly.

For example, use Customer, Sales and Quantity instead of DimCustomer, FactSales and Sum of Quantity.

Vertipaq Mode

When processing in-memory partitions, data are loaded and processed by segment. Each segment contains up to 8 millions rows. Each segment is compressed and stored in memory. Uncompressed data are deleted.

Parallel processing of partitions requires more memory than sequential processing.

The number or rows per segment can be changed by specifying a value for the server property DefaultSegmentRowCount.

To monitor memory usage by model object, we can use the following Data Management Views (DMV) tables:

SELECT * FROM $System.discover_storage_table_columns

VertiPaq Compression

VertiPaq compression algorithms aim to reduce memory usage of tabular models. There are 3 main encoding algorithms:

Value Encoding

Dictionary Encoding

Run Length Encoding (RLE)

Partitioning

Partitioning does not improve performance, but it simplifies manageability.

Its recommended to have one or many partitions with size equals to one or many segment sizes (e.g. 16M/24M/… rows).

Processing

Below SSAS processing options:

Process Clear

Drops all the data in a database, table, or partition.

Process Full

Loads data into all selected partitions or tables. Any affected calculated columns, relationships, user hierarchies, or internal engine structures (except table dictionaries) are recalculated.

Process Data

Loads data into a partition or table without recalculating calculated columns.

Process Recalc

For all tables in the database, recalculates calculated columns, rebuilds relationships, rebuilds user hierarchies, and rebuilds other internal engine structures. Table dictionaries are not affected.

Process Add

Adds rows to a partition. Any affected calculated columns, relationships, user hierarchies, or internal engine structures (except table dictionaries) are recalculated. Each Process Add creates a new segment.

Process Default

Loads data into unprocessed partitions or tables. Any affected calculated columns, relationships, user hierarchies, or internal engine structures (except table dictionaries) are recalculated.

Process Defrag

Optimizes a table dictionary (an internal engine structure) for a given table or for all tables in the database.

Use maxParallelism in the TMSL processing script to limit the number of parallel processing

{

“sequence”: {

“maxParallelism” : 2,

“operations” : [ { “refresh” : { “type” : “automatic”, “objects” : [ { “database” : “TabularProject” }]}}]

}.

Hardware Configuration

CPU and Memory performance are the most important factors when choosing a hardware.

SSAS 2016 SP1 is NUMA-aware. Being NUMA aware means that SSAS tries to reduce at a minimum the usage of the NUMA intersocket connection by preferring the usage of the local RAM bus.

Memory Management

Below server properties related to memory management:

VertiPaqPagingPolicy

Enable/disable memory paging.

VertiPaqMemoryLimit (in percentage or in number of bytes)

VertiPaq memory limit to store the data (cache excluded).

TotalMemoryLimit (in percentage or in number of bytes)

Maximum memory that can be used by the SSAS server.

LowMemoryLimit (in percentage or in number of bytes)

A lower threshold at which the server first begins releasing memory allocated to infrequently used objects.

HardMemoryLimit (in percentage or in number of bytes)

A threshold at which Analysis Services begins rejecting requests outright due to memory pressure.

We can use Performance Monitor tool to track memory usage.

Performance Monitoring

The two main tools we can use to monitor performance are Sql Profiler and Extended Events.

When using Extended Events, we need to set AutoRestart to true, so after a restart of the SSAS server, the capture of extended events automatically starts.

Direct Query Mode

In Direct Query mode, we can create Direct Query partitions and Sample partitions. Direct Query partitions are not stored in-memory. Sample partitions are In-memory partitions, and they are used only during model design. Sample partitions require processing.

From Excel, we can select between using data from Sample partitions or from Direct Query partitions. This option is available when we open Excel from a Tabular model opened in Visual Studio.

In Direct Query mode, if row-level security is defined in data source tables, then we need to configure SSAS to delegate the identity of users when querying data source tables. SSAS can impersonate a Windows user, only when Kerberos Constrained Delegation (KCD) is configured.

More details about Kerberos Constrained Delegation configuration can be found in the following link:

https://docs.microsoft.com/en-us/sql/analysis-services/instances/configure-analysis-services-for-kerberos-constrained-delegation

Row-level security can be configured in data source tables using the following TSQL commands:

CREATE FUNCTION dbo.fn_securitypredicate (@UserId INT)

RETURNS TABLE WITH SCHEMABINDING

AS

RETURN

SELECT 1 as Result WHERE @UserId = USER_NAME() –Return 1 or nothing

CREATE SECURITY POLICY fn_security

ADD FILTER /*OR BLOCK*/ PREDICATE dbo.fn_securitypredicate(UserId) on [dbo].[Table]

Direct Query Mode Limitations

Below some limitations of Direct Query Mode:

-Hierarchies are not supported in Excel, and they are ignored in MDX queries.

-Can have only one SQL data source.

-Calculated tables cannot be used.

-Some DAX functions (like ALL, CALCULATE, SUM, FILTER,…) are not supported in calculated columns.

-Some DAX functions (like TOPN, GENERATE,..) are not optimized for direct query mode, and they are not converted in corresponding SQL expressions, so they are executed inside the formula engine. As a consequence, they might require transferring large amounts of data between the source database and the SSAS engine.

-Hybrid model (In-Memory partitions + Direct Query partitions) are not supported.

Role-Based Security

In SSAS Tabular, Roles are additive.

Role filters propagate through relationships (from the one side to the many side of one-to-many relationships).

To propagate role filters from the many side to the one side of a one-to-many relationship, we need to set filter direction to Both Tables, and check the checkbox Apply the Filter Direction when using row Level Security.

Role filters cannot be applied on calculated columns when a Tabular model is In-Memory mode, because calculated columns are evaluated during model processing. In Direct Query mode, role filters are applied when querying source tables.

Dynamic Security

In the following Tabular model, we use the table Security to filter Fact table rows. The DAX filter expression is highlighted in red in the following image.

We can filter rows using an external parameter defined in the connection string. We can read the value of this parameter using the DAX function CUSTOMDATA.

Deployment

There are 4 ways to deploy a tabular model:

1-Using XMLA/TMSL

2-Using SSAS Deployment Wizard

3-Using Synchronize Wizard (Source and destination servers cannot be the same. In general, Synchronize is used to move a database from processing server to main server)

4-Backup/Restore database

.Net libraries

There are two libraries: Analysis Management Objects (AMO) and Tabular Object Model (TOM) that we can use to interact with the SSAS server.

Recommandations

Avoid large dimensions containing more than one million rows.

More articles and courses related to SSAS Tabular, Power BI and DAX can be found in the SQLBI website: http://www.sqlbi.com/.