Clean Missing Data
How estimate missing data?
We can replace missing data with the Mean, the Median or the Mode, but usually it’s not an efficient approach.
If data are multi-variable distributed as below, if there is an example (x0, ?) with a missing value y, we can estimate y as a mean of values y for examples having x near to x0.
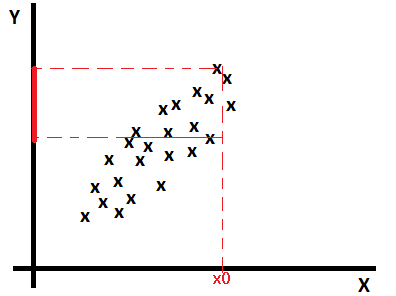
Linear regression based imputation
Find a model that estimates missing values based on other features: \(missing\_value = ?_0 + ?_1 * x_1 + ?_2 * x_2 + … + ?_{n+1} * y\)
MICE (Multiple Imputation through Chained Equations)
1-Replace all missing values with random values.
2-Pick randomly a value from one of the three nearest examples. The distance is calculated on values predicted using a regression function(linear, logistic, multinomial). Run the operation for each missing value.
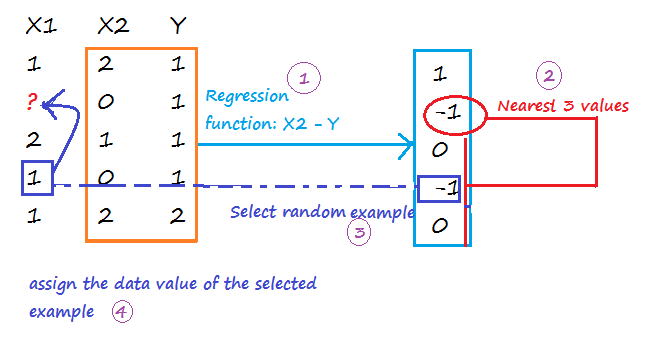
Repeat step 1 and 2 m times to create m imputed data sets. Calculate the mean of imputed values from all imputed data sets, and assign it to each missing value of the original data set.
Probabilistic PCA
The PCA approach is based on the calcul of a low-dimensional approximation of the data, from which the full data is reconstructed. The new reconstructed matrix is used to fill missing values.
Filter based Feature Selection
Pearson Correlation
Pearson correlation coefficient:
\( r_{X,Y} = \frac{Cov(X,Y)}{?_X * ?_Y} \in [-1, 1]\)Strong positive correlation when \(r_{X,Y}\) around 1.
No correlation when \(r_{X,Y}\) around 0.
Strong negative correlation when \(r_{X,Y}\) around -1.
Mutual Information
\(I(X,Y) = \sum_{x,y} p(x,y)*log(\frac{p(x,y)}{p(x)*p(y)}) >= 0\)I(X,Y) = 0 when X, Y are independent
Kendall Correlation
Kendall correlation coefficient:
\(? = \frac{C-D}{C+D} \in [-1, 1]\)C is the number of concordant pairs
D is the number of discordant pairs
|
X1 (Sorted) |
X2 |
C |
D |
|
1 |
2 |
#values{X2>2 && X1>1}=3 |
#values{X2<2 && X1>1}=1 |
|
2 |
1 |
#values{X2>1 && X1>2}=3 |
#values{X2<1 && X1<2}=0 |
|
3 |
3 |
#values{X2>3 && X1>3}=2 |
#values{X2<3 && X1<3}=0 |
|
4 |
5 |
#values{X2>5 && X1>4}=0 |
#values{X2<5 && X1<4}=1 |
|
5 |
4 |
#values{X2>4 && X1>5}=0 |
#values{X2<4 && X1<5}=0 |
|
Total |
8 |
2 |
\(? = \frac{C-D}{C+D} = 0.6\) (Good correlation)
For more details: https://www.youtube.com/watch?v=oXVxaSoY94k
Spearman Correlation
Spearman Correlation coefficient:
The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the ranked variables.
\(r_S = \frac{Cov(rg\_X,rg\_Y)}{?_{rg\_X} * ?_{rg\_X}} \in [-1, 1]\)|
X |
Y |
rg_X (X rank) |
rg_Y (Y rank) |
|
1 |
2 |
1 |
2 |
|
3 |
1 |
2 |
1 |
|
4 |
4 |
3 |
3 |
|
6 |
7 |
4 |
4 |
|
10 |
9 |
5 |
5 |
Chi-Squared
Example:
|
X1 |
X2 |
|
1 |
2 |
|
3 |
1 |
|
3 |
1 |
|
3 |
1 |
|
3 |
2 |
|
3 |
2 |
|
Occurence X1/X2 |
1 |
2 |
|
1 |
0 (3/6) |
1 (3/6) |
|
2 |
0 (0/6) |
0 (0/6) |
|
3 |
3 (15/6) |
2 (15/6) |
In bold the expected value ((row total*column total)/n).
\(\chi^2 = \frac{(1-3/6)^2}{3/6} + \frac{(0-3/6)^2}{3/6} + \frac{(3-15/6)^2}{15/6} + \frac{(2-15/6)^2}{15/6}=1.2\)Fisher Score
I don’t know the exact formula used, maybe the coefficient is calculated as below:
\( r = \frac{\sum_{i=1}^{n} (X_i – \overline{X})*(Y_i – \overline{Y})}{\sqrt{(\sum_{i=1}^{n} (X_i – \overline{X})^2) * (\sum_{i=1}^{n} (Y_i – \overline{Y})^2)}}\)http://www.wikiwand.com/en/Fisher_transformation
Count-Based
Count of values for each feature.
Skewed Data
When training data are imbalanced (skewed), machine learning algorithms tend to minimize errors for the majority classes on the detriment of minority classes. It usually produces a biased classifier that has a higher predictive accuracy over the majority classes, but poorer predictive accuracy over the minority classes.
Synthetic Minority Oversampling Technique (SMOTE)
SMOTE is an algorithm that creates extra training data by performing certain operations on real data.
Given a set S = {(0,A), (1,A), (2,A), (3,A), (4,B), (5,B)}, A is the majority class, and B the minority class. If the amount of over-sampling needed is 200% (2x) and the number of nearest neighbors is 2, then the algorithm generates new samples in the following way:
Take the difference between an example under consideration and one of its nearest neighbor. Multiply this difference by a random number between 0 and 1, and add it to the feature vector under consideration.
Existing example (4,B) –> New example (4 + 0.3*(4-5), B)
Model Evaluation
Metrics
|
Mean Absolute Error |
\(\frac{1}{m} \sum_{i=1}^{m} |y – h_?(x)|\) |
|
Root Mean Squared Error (the standard deviation of the distribution of errors) |
\(\sqrt{\frac{1}{m} \sum_{i=1}^{m} (y – h_?(x))^2} = \sqrt{J(?)}\) |
|
Relative Absolute Error |
\(\frac{\sum_{i=1}^{m} |y – h_?(x)|}{\sum_{i=1}^{m} |y – \frac{\sum_{i=1}^{m} y}{m}|}\) |
|
Relative Squared Error |
\(\frac{\sum_{i=1}^{m} (y – h_?(x))^2}{\sum_{i=1}^{m} (y – \frac{\sum_{i=1}^{m} y}{m})^2}\) |
|
Coefficient of Determination (\(R^2\)) |
1 – [Relative Squared Error] |
True Positive: \(1\{y=1, h_?(x)=1\}\)
False Positive: \(1\{y=0, h_?(x)=1\}\)
True Negative: \(1\{y=0, h_?(x)=0\}\)
False Negative:\(1\{y=1, h_?(x)=0\}\)
|
Accuracy |
\(\frac{[True Positive] + [True Negative]}{m}\) |
|
Precision |
\(\frac{[True Positive]}{[True Positive] + [False Positive]}\) |
|
Recall |
\(\frac{[True Positive]}{[True Positive] + [True Negative]}\) |
|
F1 Score |
\(2 \frac{[Precision]*[Recall]}{[Precision]+[Recall]}\) |
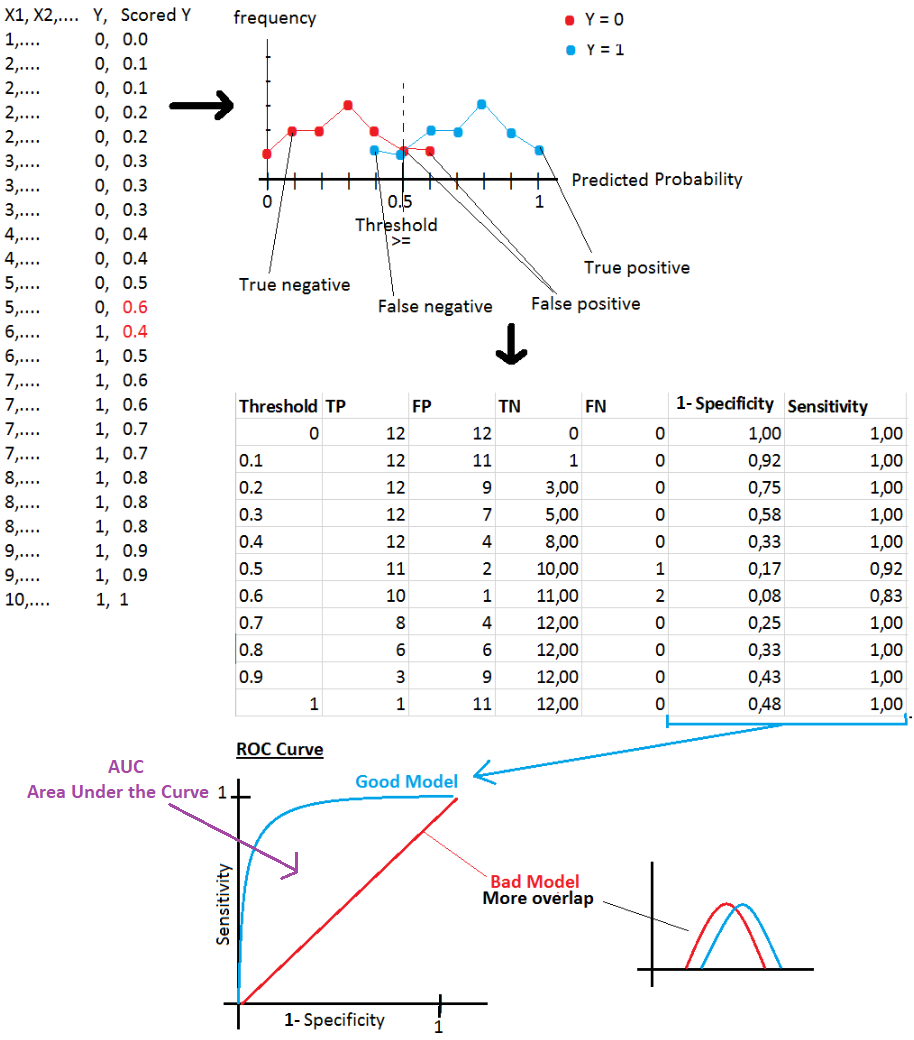
ROC Curve
Specificity: True Negative / (True Negative + False Positive)
Sensitivity: True Positive / (True Positive + False Negative)
AzureML components
Data Format Conversions
|
Convert to Dataset |
Data Input/Output
|
Enter Data Manually |
|
|
Import Data |
Import from: Azure Block Storage, Azure SQL Database, Azure Table, Hive Query, Web URL, Data Feed Provider(OData), Azure DocumentDB |
|
Export Data |
Data Transformation
|
Edit Metadata |
Rename columns |
|||||||||||||||||||||||||||||||||||
|
Join Data |
||||||||||||||||||||||||||||||||||||
|
Select Columns in Dataset |
||||||||||||||||||||||||||||||||||||
|
Remove Duplicate Rows |
||||||||||||||||||||||||||||||||||||
|
Slit Data |
||||||||||||||||||||||||||||||||||||
|
Partition and Sample |
Select Top xxx rows, or generate a sample, or split data in k folds |
|||||||||||||||||||||||||||||||||||
|
Group Data into Bins |
||||||||||||||||||||||||||||||||||||
|
Clip Value |
Remove outliers (peak and subpeak) |
|||||||||||||||||||||||||||||||||||
|
Build Counting Transform |
For each selected column, and for an output class, calculate the occurrence of a value in all rows. Example:
Note: On AzureML, we get wrong results if the number of rows is low. |
Statistical Functions
|
Summarize Data |
Machine Learning
|
Train Model |
|
|
Tune Model Hyperparameters |
Find best hyperparameter values |
|
Score Model |
|
|
Evaluate Model |
Evaluate and compare one or two scored datasets |
|
Train Clustering Model |
R/Python Language Modules
|
Create R Model |
|
|
Execute R Script |
|
|
Execute Python Script |
Supported Python packages: NumPy, pandas, SciPy, scikit-learn, matplotlib |
Machine Learning Methods
Anomaly Detection Algorithms
|
One-Class SVM |
The algorithm finds a minimal hypersphere around the data. Any point outside the hypersphere is considered an outlier. |
|
PCA-Based Anomaly Detection |
The algorithm applies PCA to reduce the dimensionality of the data, and applying distance metrics to identify cases that represent anomalies. |
Classification Algorithms
|
Logistic Regression |
|
|
Neural Network |
|
|
Averaged Perceptron |
Averaged Perceptron algorithm is an extension of the standard Perceptron algorithm; it uses averaged weights and biases. |
|
Bayes Point Machine |
It’s Bayesian linear classifier, therefore the model is not prone to overfitting |
|
Decision Forest |
|
|
Decision Jungle |
|
|
Boosted Decision Tree |
|
|
Decision Forest |
|
|
Decision Jungle |
|
|
SVM |
The algorithm finds an optimal hyperplane that categorizes new examples. I didn’t know which kernel function is used by the algorithm. Probably it uses a linear kernel \(K(x,x’) = x^T .x’)\) SVM is not recommended with large training sets, because the classification of new examples requires the computation of kernels using all training examples. |
|
Locally Deep SVM |
The algorithm defines a tree to cluster examples (like Decision Tree algorithm), and then trains SVM on each cluster. |
|
One-vs-All Multiclass |
The One-vs-All Multiclass requires as an input multiple two-class classification algorithms. To classify a new example, the algorithm runs two-class classification algorithms for each class, then select the class with higher probability. |
Clustering Algorithms
|
K-Means Clustering |
Regression Algorithms
|
Bayesian Linear Regression |
This model is not prone to overfitting |
|
Boosted Decision Tree Regression |
|
|
Decision Forest Regression |
|
|
Fast Forest Quantile Regression |
|
|
Neural Network Regression |
Neural network with an output layer having no logistic function |
|
Linear Regression |
|
|
Ordinal Regression |
Algorithm used for predicting an ordinal variable. |
|
Poisson Regression |
Algorithm used for predicting a Poisson variable |
