Linear Algebra
A matrix is a 2-D array of numbers.
A tensor is a n-D array of numbers.
Matrices are associative but not commutative.
Not all square matrices have inverse. A matrix that is not invertible is called Singular or Degenerative.
A matrix is “singular” if any of the following are true:
-Any row or column contains all zeros.
-Any two rows or columns are identical.
-Any row or column is a linear combination of other rows or columns.
A square matrix A is singular, if and only if the determinant(A) = 0
Inner product of two vectors \(\overrightarrow{u}\) and \(\overrightarrow{v}\):
\(\overrightarrow{u} * \overrightarrow{v} = p * ||\overrightarrow{u}|| = p * \sqrt{\sum_{i=1}^{n}u_{i}^{2}} = u^{T} * v = \sum_{i=1}^{n}u_{i} * v_{i}\)
p is the projection of \(\overrightarrow{v}\) on \(\overrightarrow{u}\) and \(||\overrightarrow{u}||\) is the Euclidean norm of \(\overrightarrow{u}\).
\(A = \begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix}\)
Determinant(A) = |A| = a(ei-hf) – b(di-gf) + c(dh – ge)
If \(f: R^{n*m} \mapsto R\)
\(\frac{\partial}{\partial A} f(A) = \begin{bmatrix} \frac{\partial}{\partial a_{11}}f(A) & … & \frac{\partial}{\partial a_{1m}} f(A)\\ … & … & …\\ \frac{\partial}{\partial a_{n1}}f(A) & … & \frac{\partial}{\partial a_{nm}}A\\ \end{bmatrix}\)
Example:
\( f(A) = a_{11} + … + a_{nm} \)
\(\frac{\partial}{\partial A} f(A) = \begin{bmatrix} 1 & … & 1\\ … & … & …\\ 1 & … & 1 \\ \end{bmatrix}\)
If A is a squared matrix:
trace(A) = \(\sum_{i=1}^n A_{ii}\)
trace(AB) = trace(BA)
trace(ABC) = trace(CAB) = trace(BCA)
trace(B) = trace(\(B^T\))
trace(a) = a
\(\frac{\partial}{\partial A} trace(AB) = B^T\)
\(\frac{\partial}{\partial A} trace(ABA^TC) = CAB + C^TAB^T\)
Eigenvector
Given a matrix A, if a vector μ satisfies the equation A*μ = λ*μ then μ is called an eigenvector for the matrix A, and λ is called the eigenvalue for the matrix A. The principal eigenvector for the matrix A is the eigenvalue with the largest eigenvalue.
Example:
The normalized eigenvectors for \(\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix}\) are \(\begin{bmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\) and \(\begin{bmatrix}-\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix}\), the eigenvalues are 1 and -1.
Eigendecomposition
Given a squared matrix A∈\(R^{n*n}\), ∃ Q∈\(R^{n*n}\), Λ∈\(R^{n*n}\) and Λ diagonal, such as \(A=QΛQ^T\).
Q’s columns are the eigenvectors of \(A\)
Λ is the diagonal matrix whose diagonal elements are the eigenvalues
Example:
The eigendecomposition of \(\begin{bmatrix}0 & 1 \\1 & 0 \end{bmatrix}\) is Q=\(\begin{bmatrix}\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{bmatrix}\), Λ=\(\begin{bmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{bmatrix}\)
Eigenvectors are vect
Single Value Decomposition
Given a matrix A∈\(R^{n*m}\), ∃ U∈\(R^{n*m}\), D∈\(R^{m*m}\) and D diagonal, V∈\(R^{m*m}\) such as \(A=UDV^T\).
U’s columns are the eigenvectors of \(AA^T\)
V’s columns are the eigenvectors of \(A^TA\)
Example:
The SVD decomposition of \(\begin{bmatrix} 0 & 1 \\1 & 0 \end{bmatrix}\) is U=\(\begin{bmatrix}0 & -1 \\ -1 & 0\end{bmatrix}\), D=\(\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\), V=\(\begin{bmatrix}-1 & 0 \\ 0 & -1\end{bmatrix}\).
More details about SVD can be found here: http://www.youtube.com/watch?v=9YtmGy-wfE4
The Moore-Penrose Pseudoinverse
The Moore-Penrose pseudoinverse is a matrix that can act as a partial replacement for the matrix inverse in cases where it does not exist (e.g. non-square matrices).
The pseudoinverse matrix is defined as: \(pinv(A) = \lim_{α \rightarrow 0} (A^TA + αI)^{-1} A^T\)
Analysis
0! = 1
exp(1) = 2.718
exp(0) = 1
ln(1) = 0
\(ln(x) = log_e(x) \\ log_b (b^a) = a\)
exp(a + b) = exp(a) * exp(b)
ln(a * b) = ln(a) + ln(b)
\(cos(x)^2 + sin(x)^2 = 1\)
Euler’s formula
exp(iθ) = cos(θ) + i sin(θ)
Complex numbers
Rectangular form
z = a + ib (real part + imaginary part and i an imaginary unit satisfying \(i^2 = −1\)).
Polar form
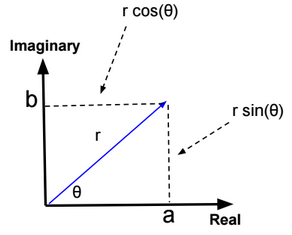
z = r (cos(θ) + i sin(θ))
Exponential form
z = r.exp(iθ)
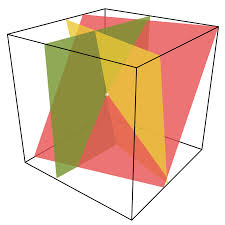
Multivariate equations
The solution set of a system of linear equations with 3 variables is the intersection of hyperplanes defined by each linear equation.
Derivatives
\(\frac{\partial f(x)}{\partial x} = \lim_{h \rightarrow 0} \frac{f(x+h) – f(x)}{h}\)
|
Function
|
Derivative
|
|
x^n
|
n * x^(n-1)
|
|
exp(x)
|
exp(x)
|
|
f o g (x)
|
g’(x) * f’ o g(x)
|
|
ln(x)
|
1/x
|
|
sin(x)
|
cos(x)
|
|
cos(x)
|
-sin(x)
|
Integration by parts
\(\int_{a}^{b} (f(x) g(x))’ dx = \int_{a}^{b} f'(x) g(x) dx+ \int_{a}^{b} f(x) g'(x) dx\)
Binomial theorem
\((x + y)^n = \sum_{k=0}^{n} C_n^k x^k y^{n-k}\)
Chain rule
Z = f(x(u,v), y(u,v))
\(\frac{\partial Z}{\partial u} = \frac{\partial Z}{\partial x} * \frac{\partial x}{\partial u} + \frac{\partial Z}{\partial y} * \frac{\partial y}{\partial u}\)
Entropy
Entropy measures the uncertainty associated with a random variable.
\(H(X) = -\sum_{i=1}^n p(x^{(i)}) log(p(x^{(i)}))\)
Example:
Entropy({1,1,1,1}) = 0
Entropy({0,1,0,1}) = -½ (4*log(½))
Hessian
\(H = \begin{bmatrix}\frac{\partial^2 f(θ)}{\partial θ_1\partial θ_1} & \frac{\partial^2 f(θ)}{\partial θ_1 \partial θ_2} \\ \frac{\partial^2 f(θ)}{\partial θ_2\partial θ_1} & \frac{\partial^2 f(θ)}{\partial θ_2\partial θ_2} \end{bmatrix}\)
Example:
\(f(θ) = θ_1^2 + θ_2^2 \\ H(f) = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}\)
A function f(θ) is convex if its Hessian matrix is positive semidefinite (\(x^T.H(θ).x >= 0\), for every \(x∈R^2\)).
\(x^T.H(θ).x = \begin{bmatrix} x_1 & x_2 \end{bmatrix} . \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} . \begin{bmatrix} x_1\\ x_2 \end{bmatrix} = 2 x_1^2 + 2 x_2^2 >= 0\)
Method of Lagrange Multipliers
To maximize/minimize f(x) with the constraints \(h_r(x) = 0\) for r in {1,..,l},
We need to define the Lagrangian: \(L(x, α) = f(x) – \sum_{r=1}^l α_r h_r(x)\) and find x, α by solving the following equations:
\(\frac{\partial L}{\partial x} = 0\)
\(\frac{\partial L}{\partial α_r} = 0\) for all r
\(h_r(x) = 0\) for all r
Calculate the Hessian matrix (f”(x)) to know if the solution is a minimum or maximum.
Method of Lagrange Multipliers with inequality constraints
To minimize f(x) with the constraints \(g_i(x) \geq 0\) for i in {1,..,k} and \(h_r(x) = 0\) for r in {1,..,l},
We need to define the Lagrangian: \(L(x, α, β) = f(w) – \sum_{i=1}^k α_i g_i(x) – \sum_{r=1}^l β_r h_r(x)\) and find x, α, β by solving the following equations:
\(\frac{\partial L}{\partial x} = 0\)
\(\frac{\partial L}{\partial α_i} = 0\) for all i
\(\frac{\partial L}{\partial β_r} = 0\) for all r
\(h_r(x) = 0\) for all r
\(g_i(x) \geq 0\) for all i
\(α_i * g_i(x) = 0\) for all i (Karush–Kuhn–Tucker conditions)
\(α_i >= 0\) for all i (KTT conditions)
Lagrange strong duality – hard to understand 🙁
Lagrange dual function \(d(α, β) = \underset{x}{min} L(x, α, β)\), and x satisfies equality and inequality constraints.
We define \(d^* = \underset{α \geq 0, β}{max}\ d(α, β)\)
We define \(p^* = \underset{w}{min}\ f(x) \) (x satisfies equality and inequality constraints)
Under certain conditions (Slater conditions: f convex,…), \(p^* = d^*\)
Jensen’s inequality
If f a convex function, and X a random variable, then f(E[X]) <= E[f(X)].
If f a concave function, and X a random variable, then f(E[X]) >= E[f(X)].
If f is strictly convex (f”(x) > 0), then f(E[X]) = E[f(X)] holds true only if X = E[X] (X is a constant).
Probability
Below the main probability theorems.
Law of total probability
If A is an arbitrary event, and B are mutually exclusive events such as \(\sum_{i=1}^{n} P(B_{i}) = 1\), then:
\(P(A) = \sum_{i=1}^{n} P(A|B_{i}) P(B_{i}) = \sum_{i=1}^{n} P(A,B_{i})\)
Example:
Suppose that 15% of the population of your country was exposed to a dangerous chemical Z. If exposure to Z quadruples the risk of lung cancer from .0001 to .0004. What’s the probability that you will get lung cancer.
P(cancer) = .15 * .0004 + .85 * .0001 = .000145
Bayes’ rule
P(A|B) = P(B|A) * P(A) / P(B)
Where A and B are events.
Example:
Suppose that 15% of the population of your country was exposed to a dangerous chemical Z. If exposure to Z quadruples the risk of lung cancer from .0001 to .0004. If you have lung cancer, what’s the probability that you were exposed to Z?
P(Z|Cancer) = P(Cancer|Z) * P(Z) / P(Cancer)
We can calculate the P(Cancer) using the law of total probability: P(Cancer) = P(Cancer|Z) * P(Z) + P(Cancer|~Z) * P(~Z)
P(Z|Cancer) = .0004 * 0.15 / (.0004 * 0.15 + .0001 * .85) = 0.41
Chain rule
\(P(A_1,A_2,…,A_n) = P(A_1) P(A_2|A_1) ….P(A_n|A_{n-1},…,A_1)\)
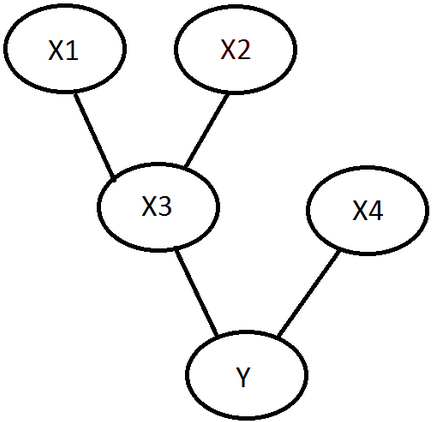
P(Y,X1,X2,X3,X4) = P(Y,X4,X3,X2,X1)
= P(Y|X4,X3,X2,X1) * P(X4|X3,X2,X1) * P(X3|X2,X1) * P(X2|X1) * P(X1)
= P(Y|X4,X3) * P(X4) * P(X3|X2,X1) * P(X2) * P(X1)
The Union Bound
\(P(A_1 \cup A_2 … \cup A_n) \leq P(A_1) + P(A_2) + … + P(A_n) \)
Nb of permutations with replacement
Nb of permutations with replacement = \({n^r}\), r the number of events, n the number of elements.
Probability = \(\frac{1}{n^r}\)
Example:
Probability of getting 3 six when rolling a dice = 1/6 * 1/6 * 1/6
Probability of getting 3 heads when flipping a coin = 1/2 * 1/2 * 1/2
Nb of permutations without replacement and with ordering
Nb of permutations without replacement = \(\frac{n!}{(n-r)!}\), r the number of events, n the number of elements.
Probability = \(\frac{(n-r)!}{n!}\)
Example:
Probability of getting 1 red ball and then 1 green ball from an urn that contains 4 balls (1 red, 1 green, 1 black and 1 blue) = 1/4 * 1/3
Nb of combinations without replacement and without ordering
Nb of combinations \(\frac{n!}{(n-r)! \, r!}\), r the number of events, n the number of elements.
Probability = \(\frac{(n-r)! \, r!}{n!}\)
Example:
Probability of getting 1 red ball and 1 green ball from an urn that contains 4 balls (1 red, 1 green, 1 black and 1 blue) = 1/4 * 1/3 + 1/4 * ⅓