I think I can safely say that nobody understands quantum mechanics. ~ Richard Feynman.
Hilbert space
Hilbert space is generalization of the Euclidean space. In a Hilbert space we can have infinite number of dimensions.
A vector in an infinite-dimensional Hilbert space is represented as an infinite vector: \((x_1, x_2, .)\).
The inner product of two vectors \(?x|y? = \sum_{i=1}^? x_i y_i\)
The norm \( ||x|| = ?x|x?^{\frac{1}{2}} = \sqrt{\sum_{i=1}^? x_i^2} < ?\)
Tensor product of two vectors \(\begin{bmatrix} a_1 \\ a_2 \end{bmatrix} ? \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} a_1 * b_1 \\ a_1 * b_2 \\ a_2 * b_1 \\ a_2 * b_2 \end{bmatrix}\)
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information. Its the analog of a bit for quantum computation. A qubit is a two-state quantum-mechanical system. The state 0 could be represented as vector \(\begin{bmatrix} 1 \\ 0 \end{bmatrix} ? |0? ? |??\) (horizontal polarization) and state 1 could be represented as orthogonal vector \(\begin{bmatrix} 0 \\ 1 \end{bmatrix} ? |1? ? |??\) (vertical polarization) .
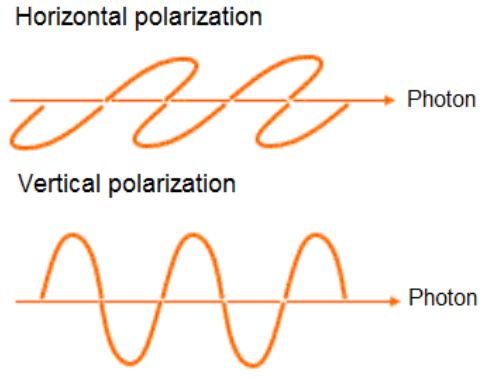
A generic qubit state corresponds to a vector \(\begin{bmatrix} ? \\ ? \end{bmatrix} = ? \begin{bmatrix} 1 \\ 0 \end{bmatrix} + ? \begin{bmatrix} 0 \\ 1 \end{bmatrix} ? ? \ |0? + ? \ |1? \) in a two-dimensional Hilbert space such as \(|?|^2 + |?|^2 = 1\) (normalized vector). \(|?|^2, |?|^2\) are the probabilities for the particle to be in state 0 and 1. ? and ? are complex numbers and they are called amplitudes.
Another way to write the state ? of a qubit is by using cos and sin functions.
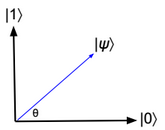
|?? = cos(?) |0? + sin(?) |1?
More details about qubit can be found here: https://arxiv.org/pdf/1312.1463.pdf
Two qubits
A state in a combined two qubits system corresponds to a vector in four-dimensional Hilbert space \(|\gamma? = e \ |00? + f \ |01? + g \ |10?+ h \ |11? = \begin{bmatrix} e \\ f \\ g \\ h \end{bmatrix} \).
In general, the state vector of two combined systems is the tensor product of the state vector of each system.
Some expressions and their equivalents:
|0??|0??|0? ? |000?
|0??|1??|0? ? |010?
\((\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?)?(\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?) ? \frac{1}{2}|00? + \frac{1}{2}|01? + \frac{1}{2}|10? + \frac{1}{2}|11?\)Bloch sphere
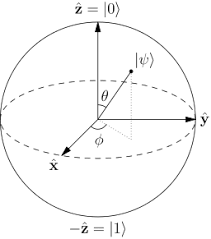
A state ? of a qubit can be also written as: \(|?? = cos(\frac{?}{2})|0? + sin(\frac{?}{2}) exp(i?) |1?\), and it can be visualized as a vector of length 1 on the Bloch sphere.
The angles ?,? correspond to the polar and azimuthal angles of spherical coordinates (??[0,?], ??[0,2?]).
Bra-ket notation
|01? ? |0??|1? ? \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \) (column vector)
?01| ? ?0|??1| ? \(\begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix} \) (row vector)
Quantum superposition
An arbitrary state of a qubit could be described as a superposition of 0 and 1 states.
N qubits
A 3 qubits quantum system can store numbers such as 3 or 7.
|011? ? |3?
|111? ? |7?
But it can also store the two numbers simultaneously using a superposition state on the last qubit.
\((\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?)?|1??|1? ? \sqrt{\frac{1}{2}} (|011? + |111?)\)In general, a quantum computer with n qubits can be in an arbitrary superposition of up to \(2^n\) different states simultaneously.
Quantum gates
Hadamard H gate
The Hadamard gate acts on a single qubit. It maps the state |0? to a superposition state with equal probabilities on state 0 and 1 (\(\sqrt{\frac{1}{2}}|0? + \sqrt{\frac{1}{2}}|1?\)).
The Hadamard matrix is defined as: \(H = \frac {1}{\sqrt {2}} \begin{bmatrix}1 \ 1 \\ 1 \ -1 \end{bmatrix}\)
\(H * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \sqrt{\frac{1}{2}} \\ \sqrt{\frac{1}{2}} \end{bmatrix}\)Pauli X gate (NOT gate)
The Pauli-X gate acts on a single qubit. It is the quantum equivalent of the NOT gate for classical computers.
The Pauli X matrix is defined as: \(X = \begin{bmatrix}0 \ 1 \\ 1 \ 0 \end{bmatrix}\)
\(X * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\)Pauli Y gate
The Pauli-Y gate acts on a single qubit. It equates to a rotation around the Y-axis of the Bloch sphere by ? radians. It maps |0? to i |1? and |1? to ?i |0?
The Pauli Y matrix is defined as: \(Y = \begin{bmatrix}0 \ -i \\ i \ 0 \end{bmatrix}\)
\(Y * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ i \end{bmatrix}\)Pauli Z gate
The Pauli-Z gate acts on a single qubit. It equates to a rotation around the Z-axis of the Bloch sphere by ? radians. It leaves the basis state |0? and maps |1? to ?|1?
The Pauli Z matrix is defined as: \(Z = \begin{bmatrix}1 \ 0 \\ 0 \ -1 \end{bmatrix}\)
\(Z * \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\)Other gates are described in this link: https://en.wikipedia.org/wiki/Quantum_gate
State measurement
State measurement can be done using polarizing filters. Filters transmit or block particles based on angle of polarization.
IBM Q
IBM Q is a cloud quantum computing platform.
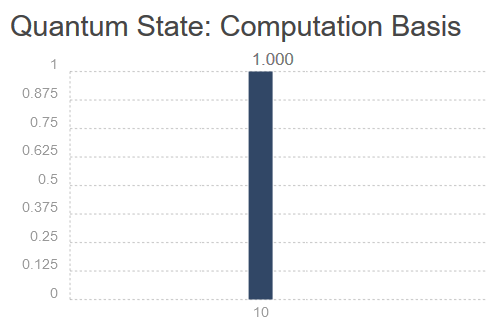
Below a simple experiment where we have two qubits. No transformation is applied on first qubit. A Pauli X transformation is applied on second qubit. As result there is one possible state |10? with probability equals 1.

Data representation
Given a vector \(x = (x_1, x_2, . , x_n)\). The quantum system topology needed to store the vector x is \(log_2(n)\) qubits.
For example, the quantum system representation of the following vector requires only 3 qubits.
(0, 0.2, 0.2, 0, 0.1, 0.2, 0.1, 0.3) ? 0 |000? + 0.2 |001? + 0.2 |010? + 0 |011? + 0.1 |100? + 0.2 |101? + 0.1 |110? + 0.3 |111?